Aufgaben zur Zentripetalkraft

Zentripetalkräfte lauern überall...

Grundlagen: Zentralkraft
Für die Zentralkraft gilt:
Fz = m ω2 r oder z=m v2 / r
Je nach Betrachtungsweise interpretieren wir diese Kraft als
- die Kraft, die die Gescheindigkeitsrichtung permanent in Richtung des Kreismittelpunktes dreht (Zentripetalkraft) oder als
- Scheinkraft, die ein Beobachter innerhalb des rotierenden Systems verspürt (Zentrifugalkraft oder Fliehkraft).

Aufgabe 1) Zentralkräfte in verschiedenen Situationen
Berechnen Sie die wirkenden Zentralkräfte in den folgenden Situationen. Vergleichen Sie mit der vorliegenden Gewichtskraft.
a) Ein Auto fährt mit 30 km/h auf einer Kurve mit dem Radius 12m. Dabei werden die Insassen (65kg) im Auto zur Seite gedrückt.
b) Ein Hammerwerfer schleudert seinen Hammer (Masse: 7.26kg,Seillänge: 1,4m ) dreimal pro Sekunde um den eigenen Körper. Mit welcher Kraft muss er ziehen?
c) Die Gewichtskraft eines 12kg schweren Körpers reduziert sich durch die Erdrotation. Berechnen Sie diese Reduzierung für einen Ort am Äquator (Erdradius 6378km) und für Berlin (52° nördlicher Breite) in Prozent.
d)* Über dem Äquator fliege ein Flugzeug in 10km Höhe mit 900km/h in Richtung Osten. Berechnen Sie die genaue Kraft in Richtung Erdmittelpunkt, die auf einen 75kg schweren Passagier wirkt

Aufgabe 2) Motorradfahrer
Ein Motorrad- oder Fahrradfahrer muss sich in einer Kurfe schräg hineinlegen.
a) Begründen Sie dies durch eine geeignete Skizze mit Kraftpfeilen. Überlegen Sie, warum die Masse des Fahrzeugs keine Rolle spielt.
b) Berechnen Sie diese Kraft für ein 270kg schweres Motorrad bei einer Geschwindigkeit von 80km/h und einem Kurvenradius von 60m. Berechnen Sie den Neigungswinkel des Motorrades.
c) Welche Kraft wirkt auf den Fahrer (70kg) ein?
d) Der Neigungswinkel zwischen Straße und Motorrad kann 30° nicht unterschreiten. Berechnen Sie die maximale Geschwindigkeit, mit der der Motorradfahrer die Kurve durchfahren kann.

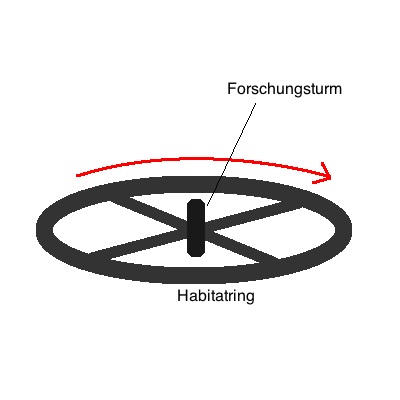Bild Aufgabe 3) Raumstation
In vielen Zukunftsromanen werden Weltraumstationen in Form eines rotierenden Torus mit Querstreben gebaut. Die dabei benötigte Zentripetalkraft simuliert dabei die Schwerkraft.
--> Gegeben sei eine Weltraumstation mit einem Durchmesser von 20m .
a) In welche Richtung wirkt die auf die Besatzung wirkende Zentripetalkraft? Wie wird die Schwerkraft simuliert?
Wo liegt demnach der Fußboden?
b) Berechnen Sie, wie schnell sich ein 2kg schwerer Körper an der Außenseite der Station bewegen müsste, damit auf ihn eine Zentripetalkraft wirkt, die der Erdanziehungskraft an der Erdoberfläche entspricht.
c) Wie lang dauert ein Umlauf um die gesamte Station? Wie würde man sich dabei fühlen? Ist es ratsam, Fenster an der Station anzubringen?
d) Wie verändert sich die Zentripetalkraft, wenn man sich entlang der Querstreben zum Forschungsturm bewegt? Berechnen Sie mehrere Werte und stellen sie sie in einem Diagramm dar.


Aufgabe 4)* verschiedene Zentripetalkräfte (nutzen ggf. Sie die Formelsammlung!)
a) Im Planetenmodell des Atoms stellt man sich vor, dass das Elektron auf einer Kreisbahn um den Atomkern kreist. Berechnen Sie für ein Wasserstoffatom (Radius: 5,3 E-11m) die wirkende Coulombkraft (Anziehungskraft verschiedener Ladungen). Diese wirkt als Zentripetalkraft. Berechnen Sie daraus die Geschwindigkeit eines Elektrons in diesem Modell. Geben sie Sie in Prozent der Lichtgeschwindigkeit an.
b) Der Abstand Erde-Mond beträgt im Mittel 374.000km. Zeigen Sie, dass man aus dieser Information die Masse der Erde bestimmen kann und berechnen Sie diese. Vergleichen Sie mit dem Literaturwert.

zurück home inhalt Lösungen