LÖSUNG

Aufgabe 1)
a) Die Zentripetalkraft ergibt sich aus:
F_z = m*v²/r = 70kg*(8,333m/s)²/12m=376,16N
Dies entspricht etwa der Hälfte der Gewichtskraft.

b) Die Zentripetalkraft ergibt sich aus:
F_z = m * ω²r = 7,26kg*(2*π*3Hz)²*1,4m = 3611N
Dies entspricht dem 50-fachen der Gewichtskraft!

c) Wähle beliebige Masse, z.B. 1kg:
Die Zentripetalkraft ergibt sich aus:
F_z = m * ω²r = 1kg*(2*π*($\frac{1\mathrm{Umlauf}}{24*60*60\sec }$)²*6.378.000m = 0,0208N
Dies ist nur ein geringer Bruchteil der Gewichtskraft.
Die Gewichtskraft an der Erdoberfläche beträgt:
F_g = m g = 9,81 m/s² * 1kg = 9,81N
Der prozentuale Anteil ergibt sich aus:
p = $\frac{F_z}{F_g}*100$= $\frac{\mathrm{0,0208}N}{\mathrm{9,81}N}*100$= 0,2%


d) Die wirkende Kraft ergibt sich aus der Differenz zwischen Gewichtskraft und Zentripetalkraft, da ein Teil der Gewichtskraft als Zentripetalkraft genutzt wird.
F = F_g - F_z
mit: r=R_erde+h_Flugzeug ergibt sich eine Gewichtskraft von:
F_g= G$\frac{\mathrm{Mm}}{r^2}$ = 728,684N
Die Zentripetalkraft beträgt:
F_z= m v²/r = 2,534N
Die Differenz beträgt damit:
F= 726,15N

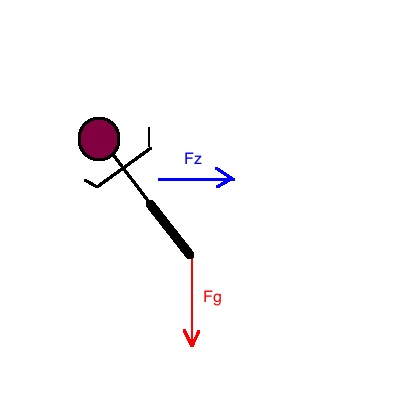Aufgabe 2) Motorrad
a) Zusätzlich zur Gewichtskraft muss der Motorradfahrer eine Zentripetalkraft aufbringen. Damit er nicht umfällt muss er in die entgegengesetzte Richtung kippen.
Die Masse spielt keine Rolle, da sowohl Gewichtskraft als auch Zentripetalkraft proportional zur Masse sind. Daher heben sich die Massen gegenseitig auf.


b) Wir berechnen den Winkel aus dem Kräfteparallelogramm:

F_z= m v²/r =2222,22N
F_g= m g = 2648,7N

Wir nutzen die Definition des Tangens:
tan(β) = $\frac{F_g}{F_z}$=> β=40°
c) Im rechtwinkligen Kräftedreieck wenden wir den Pythagoras an:
F=$\sqrt{{F_z}^2+{F_g}^2}$= 896N

d) Wie in b) gilt für das Kräfteparallelogramm:

tan(β) = $\frac{F_g}{F_z}$=> F_z-max= F_g/tan(β) = 4588N
Aus der Gleichung für die Zentripetalkraft ergibt sich:
F_z= m v²/r
v = $\sqrt{F_{z-max}r/m}$= 31,93m/s = 115km/h

Aufgabe 3)
a) Die Zentripetalkraft ist die Kraft, mit der die Querstreben die Station zusammenhalten. Sie wirkt also nach innen. Der Fußboden muss sich an der Außenwand befinden.
b) Die Zentripetalkraft soll der Gewichtskraft entsprechen.
F_g = F_z
mg = m v²/r
=> v = $\sqrt{F_{g}r/m}$= 9,9m/s
c) Die Geschwindigkeit entspricht dem Umfang geteilt durch die Umlaufzeit:
v = U/T
=> T = 2πr/v = 6,34s

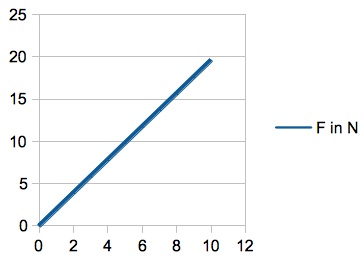
d) siehe nebenstehendes Diagramm

Aufgabe 4)
a) Hier wirkt die Coulombkraft als Zentripetalkraft:
F_z=F_c also
m v²/r = $\frac{1}{4\mathrm{\pi \epsilon }}\frac{Q1Q2}{r^2}$
=> v = 2,18E9 m/s oder 728% von c!!!!!!

b) Die Gravitationskraft wirkt als Zentripetalkraft:
F_g=F_z also
m ω²r = G$\frac{\mathrm{Mm}}{r^2}$
m (Mondmasse) fällt heraus.
Stellen wir nach der Erdmasse um, so ergibt sich:
M = ω² r³ / G = 5,71E24kg
Dies entspricht etwa dem Literaturwert.

zurück home inhalt pdf