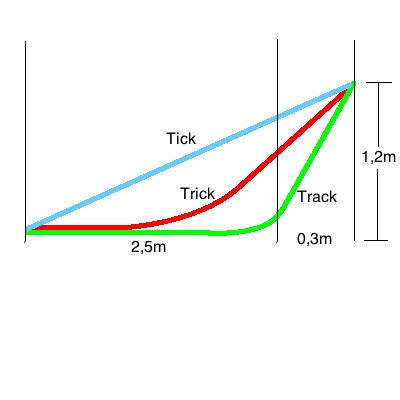
Aufgabe: Carrerabahn
Trix und Trax haben jeweils eine eigenene Carrerabahn aufgebaut und
lassen ihre Autos um die Wette fahren. Mit Hilfe von Daniel Düsentriebs
Wunderspray fahren sie alle völlig reibungsfrei.
a) Begründen Sie, warum alle Autos (ohne besondere Betrachtung der
Räder - siehe d) mit der gleichen Geschwindigkeit durch das Ziel fahren
und berechnen sie diese.
b) Konstruieren Sie zeichnerisch die Hangabtriebskraft am Start für die
einzelnen Fahrzeuge und berechnen Sie die Beschleunigungen.
c) Berechnen Sie die Fahrzeiten bis zur ersten Markierung.
Tatsächlich haben die Autos im Ziel trotz Reibungsfreiheit
unterschiedliche Geschwindigkeiten.
d) Begründen Sie dies durch einbeziehung der Räderbewegung.
e) Berechnen Sie die unterschiedlichen Geschwindigkeiten im Ziel.
f) Welcher prozentuale Anteil der Bewegungsenergie steckt in der
Rotationsbewegung der Räder?
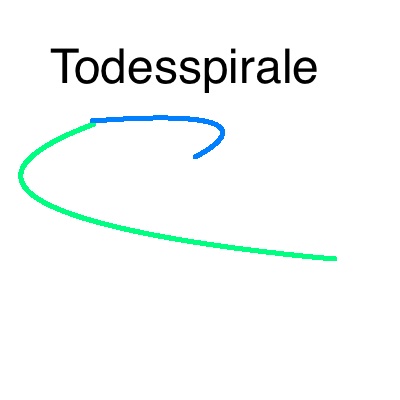
Nach der Abfahrt durchfahren alle Wagen die Todesspirale, die aus zwei
liegenden Halbkreisen mit einem großen und einem kleineren Radius
besteht.
g) Berechnen Sie den Drehimpuls und die Winkelgeschwindigkeit beim
Eintritt in die Todesspirale.
h) Berechnen Sie nun aus der Drehimpulserhaltung die
Winkelgeschwindigkeit und Geschwindigkeit in der zweiten Hälfte der
Todesspirale.
Am Ende der Todesspirale treffen die Autos von Trick und Track unter
einem Winkel von 30° aufeinander. Nach dem Zusammenstoß bilden Sie
einen Winkel von 90°
i) Konstruieren Sie den Gesamtimpuls der Wagen.
j) Konstruieren Sie eine mögliche Lösung nach dem Zusammenstoß und
entscheiden Sie, ob es sich um einen elastischen, unelastischen oder
unmöglichen Stoß handelt.
| Tick | Trick | Track | |
| Neigungswinkel der Bahn am Start | 20° | 45° | 60° |
| Masse des Wagens | 250g | 300g | 175g |
| Masse der Räder (Hohlzylinder) | 30g | 120g | 4g |
| Radius der Räder | 1,2cm | 2,5cm | 0,8cm |