Darstellung von Schwingungen

... mit Hilfe von Geogebra

Grundlagen: Umgang mit Geogebra
Geogebra enthält einen Grafikrechner, mit dem mathematische Funktionen leicht gezeichnet werden können.
Dazu werden diese Funktionen links in einer Liste eingezeichnet und erscheinen dann automatisch als graph im rechten Fenster.
Die Funktionen erhalten dann unterschiedliche Namen in alphabetischer Reihenfolge, also f(x), g(x), h(x) ...

Man kann die aufgelisteten Funktionen miteinaner kombinieren, z.B. durch Addition (f+g) oder Multiplikation (f*g).

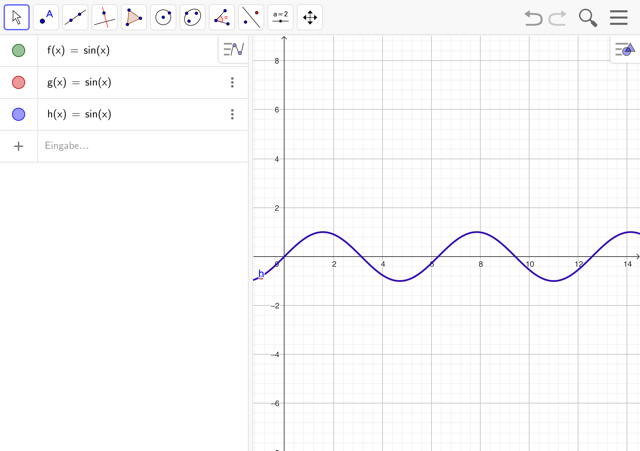
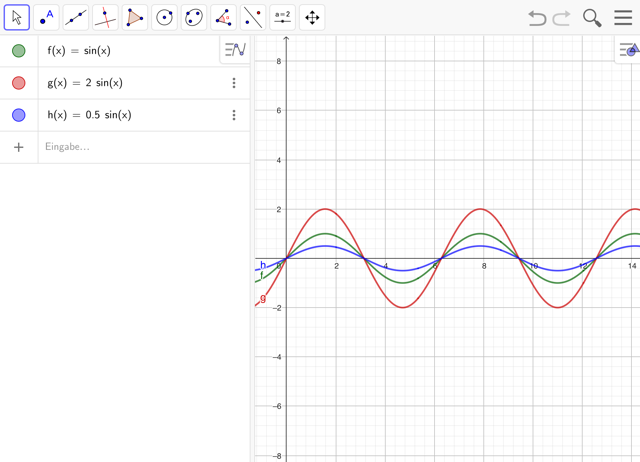
Aufgabe 1: Verschiedene Sinuskurven darstellen Erstelle mehrere Sinusfunktionen der Form sin(x). Die erste Funktion dient immer als Referenz und wird im folgenden nicht mehr verändert. Ergänze bei den weiteren Funktionen nun unterschiedliche Amplituden (z.B. 2*sin(x) )und beschreibe die Auswirkung. Wähle insbesondere auch Werte größer 1, zwischen 0 und 1 sowie negative Werte. Lösche nun alle Amplituden, so dass wieder lauter einheitliche Sinusfunktionen dastehen. Die erste Funktion bleibt wieder unverändert. 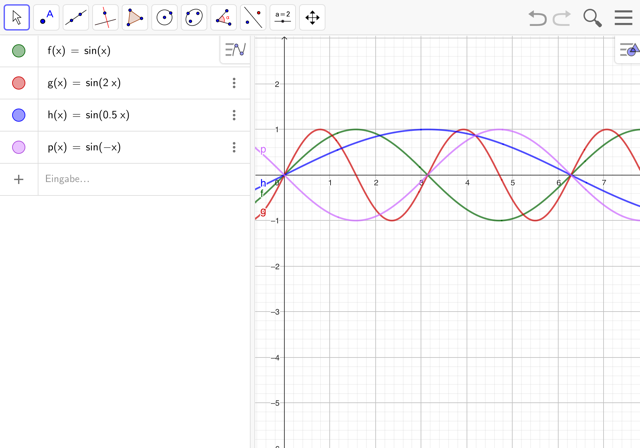Ergänze nun unterschiedliche Frequenzen (z.B. sin(2x) ) und beschreibe die Auswirkung. Wähle insbesondere auch Werte größer 1, zwischen 0 und 1 sowie negative Werte. 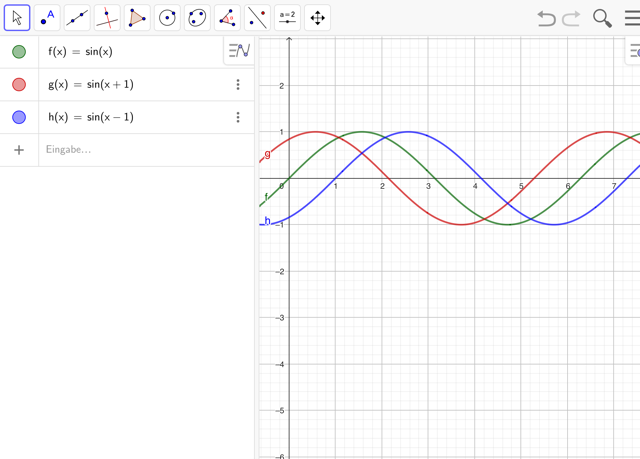Setze die Funktionen wieder wie oben zurück, indem du die Frequenzen löschst. Ergänze nun (nur nicht bei der ersten Funktion!) unterschiedliche Phasenverschiebungen (z.B. sin(x+2) und beschreibe die Auswirkung. Wähle insbesondere auch negative Werte.

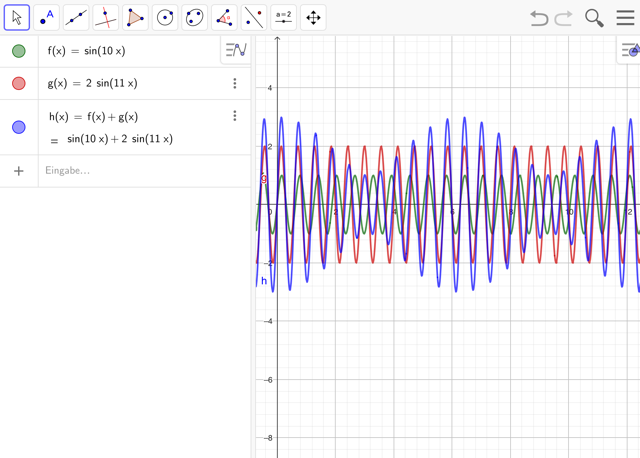
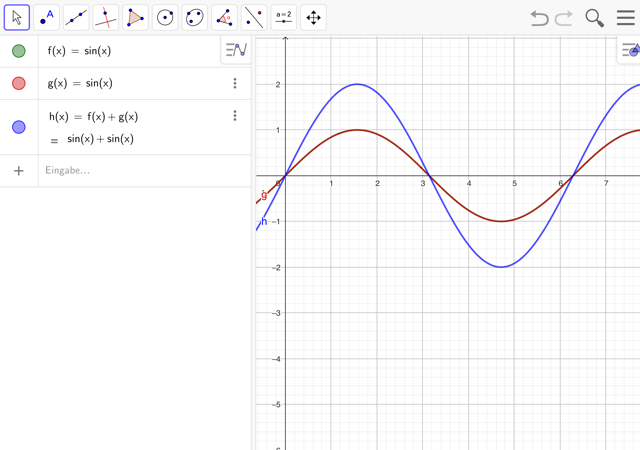
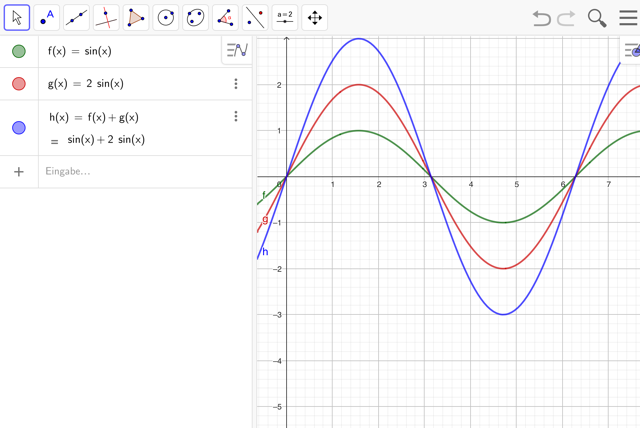
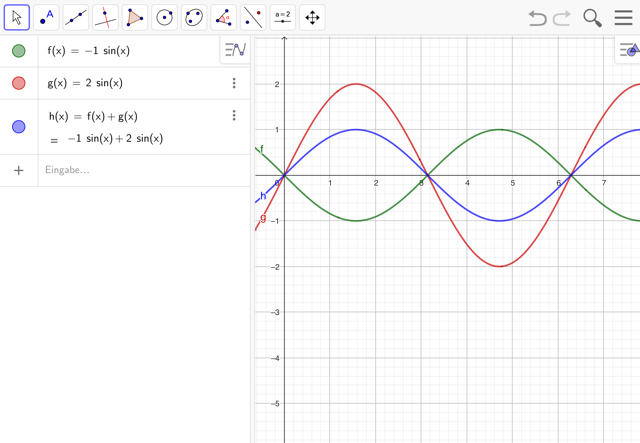
Aufgabe 2: Schwingungen überlagern (addieren) Dies entspricht dem Erklingen von mehreren Tönen gleichzeitig. Erstelle zwei Sinusfunktionen der Form sin(x) und eine dritte Funktion, in der beide Funktionen addiert werden (f+g). Gebe den Sinusfunktionen nun unterschiedliche Amplituden. Beschreibe was geschieht. Wähle insbesondere auch für eine Funktion eine negative Amplitude. * Wandle die eine Funktion in eine Cosinusfunktion um und beobachte nochmal, was geschieht. 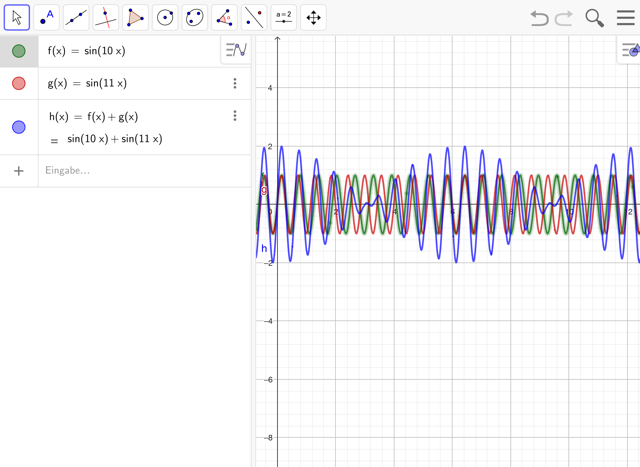Setze die Funktionen zurück und wähle nun unterschiedliche Frequenzen. Beschreibe was geschieht. * Untersuche auch, was geschieht, wenn die Schwingungen unterschiedliche Amplituden haben. Setze die Funktionen zurück und gebe der zweiten eine Phasenverschiebung. Beschreibe was geschieht. Spiele mehrere Werte zwischen -2π und 2π durch.

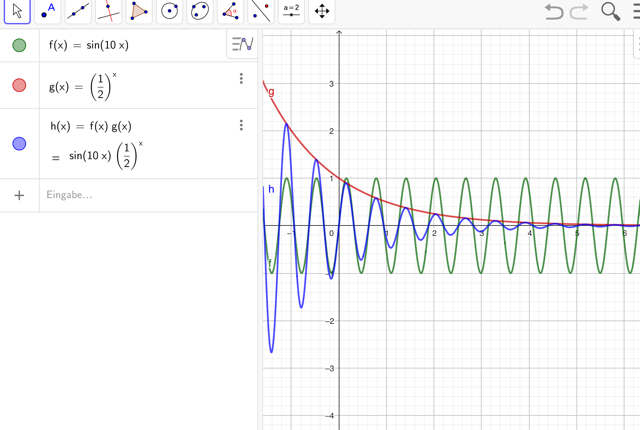
Aufgabe 3: Schwingungen einhüllen (multiplizieren) Erstelle eine Sinusfunktionen und eine Exponentialfunktion der Form $g\left(x\right) = {\left(\frac{1}{2}\right)}^x$ Multipliziere beide Funktionen miteinander (f*g) und beobachte was geschieht. Gebe der Exponentialfunktion verschiedene Parameter im Exponenten (z.B. $g\left(x\right) = {\left(\frac{1}{2}\right)}^{\mathrm{2x}}$) und beobachte die Auswirkungen. Wähle auch negative Werte.

zurück home inhalt Lösung