Aufgaben zur Dichte

Grundlagen: Die mathematische Definition der Dichte
Die Dichte sagt aus, welche Masse ein Körper pro Volumen hat. Mathematisch entspricht dies dem Quotienten aus Masse und Volumen:
Dichte = $\frac{\mathrm{Masse}}{\mathrm{Volumen}}$
Sind zwei der Größen angegeben, kann man entsprechend die dritte Größe ausrechnen.

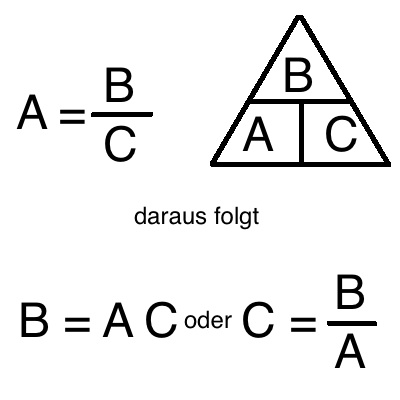
Umstellen der Gleichung: Wie löst man nach dem Volume oder der Masse auf? Mit der oben angegebenen Gleichung kann man die Dichte selber ausrechnen. Möchte man aber die Masse oder das Volumen ausrechnen, so ist eine Umstellung nötig. Dazu kann man den "Dreieckstrick" benutzen: - Man schreibt alle Größen in ein Dreiech, so dass die Größe aus dem Nenner in der Spitze des Dreieckes steht. Die beiden anderen stehen unten nebeneinander. - Nun kann man umstellen. Entweder liest man das Dreieck zeilenweise oder eine der unteren Ecken wird gesucht, dann schreibt man die anderen beiden als Bruch. (Siehe Kasten)

Aufgabe 1) Umstellen der Gleichung
a) Zeichne das Dreieck mit allen drei Größen für die Gleichung der Dichte auf.
b) Löse die Gleichung nach allen drei Größen auf. Schreibe alle drei Gleichungen auf.

Notieren einer Rechenaufgabe:
- Schreibe in den folgenden Aufgaben zunächst die gesuchte Größe und die gegebenen Größen auf.
- Dann schreibst Du die benötigte Gleichungsform auf.
- Schließlich ersetzt Du die gegebenen Größen durch ihre Werte und rechnest das Ergebnis aus.

Aufgabe 2) Die Dichte-Gleichung in allen Variationen
a) Ein Stein hat ein Volumen von 12cm³. Er wiegt 36g. Berechne die Dichte des Steines.
b) Ein anderer Stein der gleichen Sorte wiegt 60g. Berechne sein Volumen.
c) Welche Masse muss ein Stein dieser Sorte haben, wenn er ein Volumen von 15cm³ haben soll?

Aufgabe 3) Luft - so gut wie nichts?
Luft hat wie alle Gase eine geringe Dichte. Allerdings ist es ein Irrtum anzunehmen, dass sie so gut wie nichts wiegt, wie die folgende Aufgabe zeigen wird.
a) Ein Liter Luft wiegt ca. 1,2 g. Überlege Dir wie viele Kubikcentimeter in einen Liter hineinpassen und rechne dann die Dichte aus.
b) Ein Sitzball hat ein Volumen von 800 Litern. Seine Gummihülle wiegt 350g. Berechne die gesamte Masse des Balles.
c) Damit der Ball nicht in sich zusammenfällt, muss die in ihm enthaltene Luft einen höheren Luftdruck haben. Die Luft wurde auf das doppelte ihres Ausgangszustandes zusammengedrückt. Berechne die neue Masse des Balles.
d) Warum kann man nicht sagen, dass Luft nichts wiegt?

zurück home inhalt Lösungen