Die Heisenbergsche Unschärferelation
Lassen sich Ort und Bewegung beliebig genau bestimmen?
Grundlagen: Unschärfe von Ort und Impuls
In unserer makroskopischen Welt sind Ort und Bewegung völlig unabhängig
voneinander. Wir meinen die Position eines Objektes (genauer seines
Schwerpunktes) und seine Bewegung (genauer seinen Geschwindigkeits- oder
Impulsvektor) beliebig genau kennen zu können. Sie beeinflussen sich nicht
gegenseitig.
In kleinen Maßstäben tritt aber der Wellencharakter von Teilchen immer stärker
hervor. Und diesbezüglich gelten auch hier enge Verflechtungen zwischen Ort und
Impuls.
Heisenbergsche Unschärferelation
Heisenberg postulierte, dass die genauigkeit einer Ortsbestimmung und
die Genauigkeit einer Impulsbestimmung eng miteinander zusammenhängen.
Insbesondere gilt:
Δx Δp > h/4π
D.h. je genauer man einen Ort kennt (kleines Δx) desto ungenauer
ist seine Bewegungsrichtung festgelegt (großes Δp)
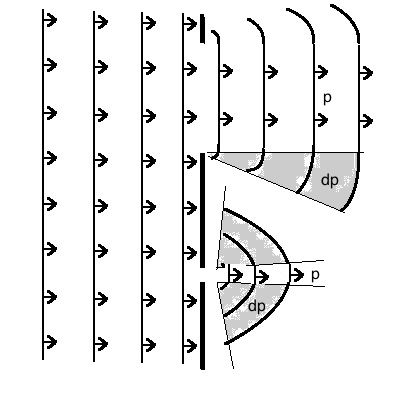
Dies findet seine Entsprechung in Wellenphänomenen. Trifft eine Welle
auf einen im Vergleich zu ihrer Wellenlänge großen Spalt, so findet
keine wesentliche Streuung statt. Ist dagegen der Spalt gleich oder
kleiner der Wellenlänge, so ist die Streuung erheblich. |
 gif
gif
gif
gif
|
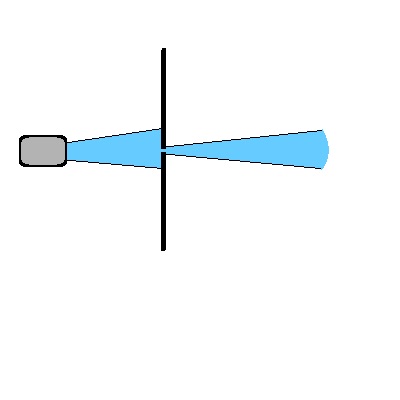
Aufgabe 1) Elektronenstrahl
In einer Elektronenkanone soll ein möglichst scharf gebündelter gerader
Elektronenstrahl entstehen. Dazu werden Beschleunigungselektroden mit
Löchern der Durchmesser 1nm, 0,5nm und 0,2nm getestet. Die
Beschleunigungsspannung beträgt 3V bzw. 30V.
a) Berechnen Sie den Impuls und die Impulsunschärfe der Elektronen nach
der Beschleunigungskanone.
b) Berechnen Sie den Öffnungswinkel des Elektronenstrahls.
c) Was bedeutet dieses Phänomen für die Schärfe eines Fernsehbildes, wenn es durch einen Elektronenstrahl erzeugt wurde?
|
|
Aufgabe 2) Beispiele in verschiedenen
Größenordnungen
a) Heisenberg geriet in eine Radarfalle. Er sei 123,456789km/h mit seinem
456,7890123kg schweren und 2,3456789m breiten Auto gefahren.
Kann sich Heisenberg mit seiner Unschärferelation herausreden?
b) Ein Tröpfchen der Masse 2pg und dem Durchmesser 10nm bewege sich mit 1,5m/s
durch die Luft. Spielt die Impulsunschärfe eine Rolle?
c) In einem Atom habe ein Elektron eine kinetische Energie von 1,5eV. Es ist in
einer Kugel mit dem Durchmesser 1E-10m eingesperrt. Was kann man über die
Bewegungsrichtung des Elektrons aussagen?
zurück home inhalt Lösungen
 gif
gif
gif
gif
