Aufgabe zum Schwingkreis

Fragestellung

Grundlagen:
ohmsches Gesetz: U = R I
Energieinhalt von Spule und Kondensator: W_L = 1/2 L I² W_C= 1/2 C U²
Thompsonsche Schwingungsgleichung: T = 2π$\sqrt{\mathrm{LC}}$
für einen gedämpften Schwingkreis gilt: f = $\frac{1}{2\pi }\sqrt{\frac{1}{\mathrm{LC}}-\frac{R^2}{4L^2}}$

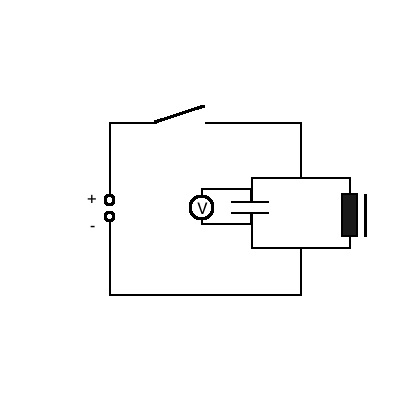
Aufgabe 1) Sekundenschwingkreis An eine Spule mit 630H und einen Kondensator mit 40μF wird eine Spannung von 2 V angelegt. Anschließend wird durch Öffnen des Schalters eine elektromagnetische Schwingung erzeugt. Da die Spule aus einem langen dünnen Draht besteht, hat sie einen nicht vermeidbaren ohmschen Widerstand von 1000Ω. a) Berechnen Sie den maximalen Strom durch die Spule bei geschlossenem Schalter. b) Berechnen Sie die in Kondensator und Spule gespeicherte Gesamtenergie. c) Wäre der Schwingkreis verlustfrei, so müsste eine so hohe Selbstinduktionsspannung entstehen, dass die gesamte Energie in den Kondensator fließen würde. Berechnen Sie diese (theoretische) Spannung. d) Tatsächlich wird beim ersten Ausschlag (Kondensator ist maximal aufgeladen) nur eine Spannung von -6V gemessen. Wie viel Prozent der Energie sind also während des ersten "Anstoßens" verloren gegangen?

Aufgabe 2) Hochfrequenzschwingkreis
Gegeben ist ein Kondensator der Kapazität 5μF und eine Spule der Induktivität 12mH. Sie bilden einen - zunächst ungedämpften - Schwingkreis.
a) Berechnen Sie die Eigenfrequenz dieses Schwingkreises.
b) Wie müsste man die Induktivität oder Kapazität verändern, um eine Frequenz von 1kHz zu erhalten?
Die Spule habe einen ohmschen Widerstand von 50 Ohm
c) Um wie viel Prozent weicht die Eigenfrequent nun von der ungedämpften ab?
d) Welchen Wert kann der Widerstand maximal annehmen? Welche Bedeutung hat es, wenn er diesen Wert übersteigt?

zurück home inhalt Lösungen