Lorentzkraft einfach und vektoriell

Rechnungen mit dem Kreuzprodukt

Grundlagen: Lorentzkraft als Kreuzprodukt
$\vec{F_{L}} = \vec{IΔs} \otimes \vec{B}$ oder F_L = I Δs B sinα auf Ströme
$\vec{F_{L}}$ = Q $\vec{v} \otimes \vec{B}$ oder F_L = Q v B sinα auf einzelne Ladungen.
Magnetfeld um einen stromdurchflossenen Leiter: B = μ₀ I/2πr

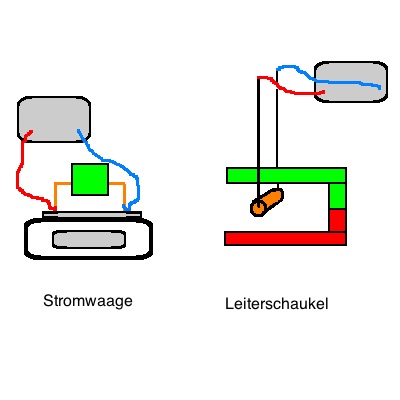
Aufgabe 1) Stromwaage und Leiterschaukel
In einem horizontal verlaufenden homogenen Magnetfeld der Stärke 320 mT befinde sich ein horizontal verlaufender 12cm langer Draht auf einer präzisen Waage. Durch ihn fließe ein Strom der Stärke 2A.
a) Bestimmen Sie die Massenänderung, die beim Einschalten des Stromes auf der Waage angezeigt wird.

Das Drahtstück hänge nun in dem Magnetfeld wie an einer Schaukel. Es habe eine Masse von 40g, die Masse der zuführenden Drähte sein vernachlässigbar.
b) Berechnen Sie den Winkel, um den diese Leiterschaukel aus ihrer Ruhelage ausgelenkt wird.

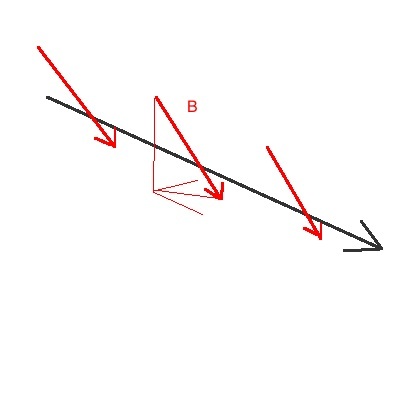
Aufgabe 2) Überlandleitungen
Eine Starkstromleitung führe 2km nach Osten und 3km nach Norden. Sie trage einen Strom von 300A.
Am Ort der Überlandleitung existiert ein Erdmagnetfeld mit einer horizontalen Komponente von 32mT in Nordrichtung und einer vertikalen Komponente von 5,7mT nach unten.
a) Erstellen Sie die Vektoren $\vec{B}$ und $\vec{IΔs}$
b) Bestimmen Sie den Kraftvektor $\vec{F_{L}}$ und den Betrag und die Richtung der Kraft F_L.
Zwei solche Starkstromleitungen liegen in einem Abstand von 3m nebeneinander.
c) Bestimmen Sie die Kräfte der Leitungen aufeinander.

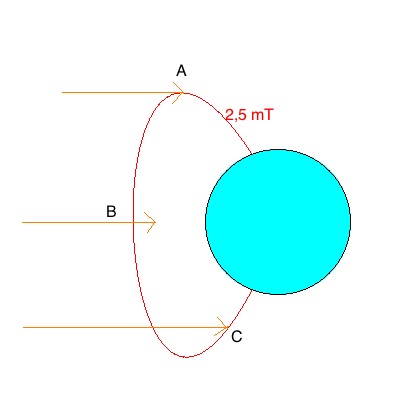
Aufgabe 3) Sonnenwind
Von der Sonne trifft ein kontinuierlicher Strom an Elementarteilchen (hauptsächlich Protonen und Elektronen) auf die Erde. Sie treffen mit einer Geschwindigkeit von ca. 0,3c auf das Magnetfeld der Erde und werden dort abgelenkt.
a) Berechnen Sie für die drei abgegebenen Punkte die Lorentzkraft mit Hilfe des Kreuzproduktes. Überprüfen Sie mit der Drei-Finger-Regel.
b) Begründen Sie, warum das Magnetfeld der Erde uns vor dem Sonnenwind schützt. Gilt dies für alle Teilchen gleichermaßen?

zurück home inhalt Lösungen