Aufgaben zu Elektronen im Magnetfeld

Grundlagen:
Lorenzkraft: F = q • v • B
Für die Richtung der Kraft gilt die Drei-Finger-Regel der rechten oder linken Hand.
Zentripetalkraft: $F=\frac{m•v^2}{r}$
kinetische Energie: $W=\frac{1}{2}m•v^2$
elektrische Energie W = q•U

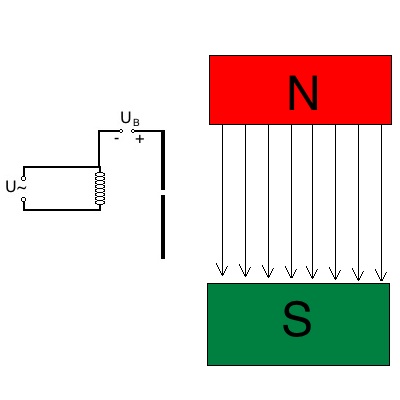
Aufgabe 1): Ablenkung eines Elektronenstrahls in einem Magnetfeld Ein Elektron wird von der Elektronenkanone mit einer Spannung von 330V beschleunigt. Es durchläuft ein Magnetfeld der Stärke 400mT. Das Magnetfeld hat eine Querschnittsfläche von 20x20 cm. a) Berechnen Sie die Geschwindigkeit des Elektrons vor Eintritt in das Magnetfeld. b) Warum ändert sich der Betrag der Geschwindigkeit im Magnetfeld nicht? Begründen Sie mit Hilfe der Kraftrichtung. c) Wie groß ist der Radius der Kreisbahn? Hinweis: Für eine Kreisbahn muss die Lorenzkraft gerade die Zentripetalkraft sein. d) Wie verändert sich der Radius der Kreisbahn, wenn man - die Beschleunigungsspannung erhöht? - die Magnetfeldstärke erhöht? e) Wie groß muss die Geschwindigkeit des Elektrons mindestens sein, damit es noch aus dem Magnetfeld heraustreten kann?

Aufgabe 2) e/m - Bestimmung:
Diesen Aufbau nutzt man, um das Verhältnis von Elektronenmasse und Elektronenladung zu ermitteln. Vollziehen Sie den Rechenweg folgendermaßen nach:
a) Stellen Sie durch Gleichsetzung der Kräfte eine Gleichung auf, mit der Sie das Verhältnis e/m berechnen können. Von welchen Größen ist e/m nun scheinbar abhängig?
b) Stellen Sie aus den Energien eine Gleichung auf, mit der Sie die Geschwindigkeit der Elektronen berechnen können.
c) Setzen Sie das Ergebnis aus b) in a) ein und formen Sie solange um, bis Sie wieder eine Gleichung für e/m haben. Wovon hängt diese nun ab?
d) In einer Messung erhalten wir für eine Beschleunigungsspannung von 550V und ein Magnetfeld von 30mT einen Radius von 0,3 cm. Ermitteln Sie das Verhältnis e/m und vergleichen Sie es mit dem Literaturwert.

zurück home inhalt Lösungen