Aufgaben Elektron in der Braunschen Röhre

Grundlagen: Für die Aufgabe werden die folgenden Formeln benötigt:

kinetische Energie: $W=\frac{1}{2}m•v^2$	elektrische Energie W = q•U
Kraftdefinition nach Newton: F = m•a	elektrische Kraft: F = q•E Elektrisches Feld: $E=\frac{U}{d}$
Für unbeschleunigte Bewegungen gilt: $v=\frac{s}{t}$	Für beschleunigte Bewegungen gilt: v = a•t $s=\frac{1}{2}a•t^2$

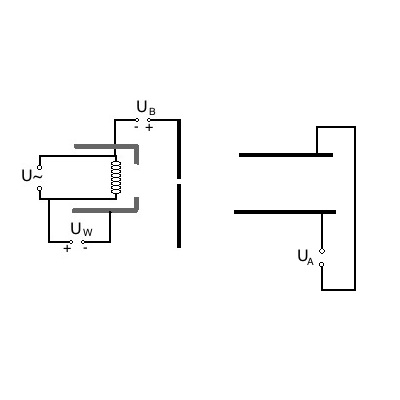
Versuchsaufbau: Für die folgenden Aufgaben gilt der übliche Aufbau einer Braunschen Röhre. Als Betriebsspannungen werden verwendet: Beschleunigungsspannung UB=270V Ablenkspannung UA=25V Für den Ablenkkondensator gilt: Abstand der Platten in vertikaler Richtung: d = 6 mm Länge der Platten in Bewegungsrichtung der Elektronen: l = 1,2 cm

Aufgabe 1)
Berechnen Sie die Geschwindigkeit, mit der die Elektronen aus der Elektronenkanone austreten.
Gehen sie davon aus, dass elektrische Energie in kinetische umgewandelt wird.

Aufgabe 2)
Berechnen Sie die Zeit, die die Elektronen benötigen, um die Ablenkelektrode in horizontaler Richtung zu durchlaufen.
Gehen Sie davon aus, dass die Elektronen die Elektrode mit konstanter Geschwindigkeit durchlaufen.

Aufgabe 3)
a) Berechnen Sie die Feldstärke im Inneren des Ablenkkondensators.
b) Berechnen sie die auf die Elektronen wirkende Kraft.
c) Berechnen Sie die auf die Elektronen wirkende Beschleunigung. Geben sie diese auch im Vielfachen der Erdbeschleunigung an.
d) Warum kann eine so kleine Kraft eine so große Beschleunigung verursachen?
e) Warum bewirkt die sehr große Beschleunigung nicht, dass das Elekton sofort auf die positive Elektode gezogen wird sondern in einem Bogen hindurchfliegt?

Aufgabe 4) Für diesen Aufgabenteil unterteilen wir die tatsächliche Geschwindigkeit der Elektronen am Ende der Ablenkelektrode in einen horizontalen und einen vertikalen Teil.
a) Zeichnen Sie ein Pfeildiagramm aus horizontaler, vertikaler und resultierender Geschwindigkeit.
b) Berechnen Sie die Geschwindigkeit, die die Elektronen in vertikaler Richtung haben, wenn sie aus der Elektronenkanone austreten.
c) Berechnen Sie die resultierende Geschwindigkeit.
d) Berechnen Sie den Austrittswinkel des Elektronenstrahls.
e) Berechnen Sie die Strecke, um die der Elektronenstrahl am Ende der Ablenkelektroden von seiner ursprünglichen Bahn abweicht.

Aufgabe 5) Funktionsgleichung
a) Erstellen Sie für den Bereich zwischen den Platten eine Funktionsgleichung und diskutieren Sie diese.
b) Erweitern Sie diese Funktionsgleichung für einen Aufbau, in dem sich hinter dem Ablenkkondensator un einiger Entfernung ein Schirm befindet.

zurück home inhalt Lösungen