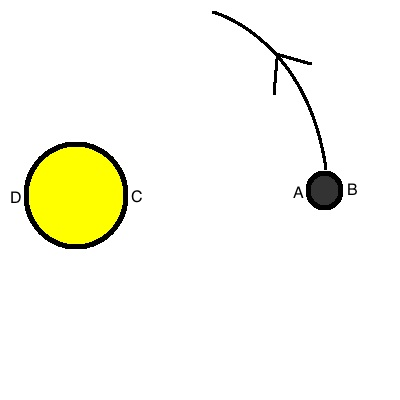
Ein Stern mit der Massen m1=2 E+33 kg wird von einem Neutronenstern der Masse m2= 3 E+31 kg in einem Abstand von 4 E+5 km umkreist. Der Neutronenstern hat einen Durchmesser von 5.000km, der Stern einen Durchmesser von 6E +4 km
a) Berechnen Sie die Position des Schwerpunktes. Fertigen Sie eine Skizze der Bewegung an.
b) Berechnen Sie die Umlaufzeit, mit der der kleinere Stern den größeren umkreist. (Hier ist der Abstand der Sterne voneinander maßgeblich, nicht der Abstand zum Schwerpunkt!)
c) Berechnen Sie die Gravitationskräfte auf eine 2 kg schwere Masse an den Punkten A und B des Neutronensterns.
d) Berechnen Sie die Zentrifugalkräfte auf eine 2kg schwere Masse an den Punkten C und D des Sterns. Zeichnen Sie eine Skizze des Sterns mit diesen Kräften.
e) Der Stern werde noch von einem zweiten Objekt auf einer elliptischen Umlaufbahn begleitet, die eine große Halbachse von 9 E+8 km hat. Berechnen Sie die Umlaufzeit dieses Objektes.
f) Wie groß ist die größte Entfernung zur Sonne, wenn er sich am sonnennächsten Punkt in einer Entfernung von 2 E+6 km befindet?
g) Wie groß müsste seine Geschwindigkeit sein, damit er sich am sonnenfernsten Punkt auf einer kreisförmigen Umlaufbahn befindet?
h) Nimmt die Geschwindigkeit zur Sonne hin zu oder ab? Argumentieren Sie sowohl über einen Kraft- als auch über einen Energieansatz und über die Kepplerschen Gesetze.