Aufgaben zu Satelliten- und Planetenbahnen

Wie schnell muss ein Körper sein, um einen anderen umkreisen zu können?

Grundlagen: Gravitationsgesetz und Zentripetalkraft
F_G = G$\frac{\mathrm{mM}}{r^2}$ und F_z = m ω²r = m v²/r
Erdmasse: 5,973 E24kg
Erdradius: 6.371km
G=6,67 E-11 m³ / kg s²

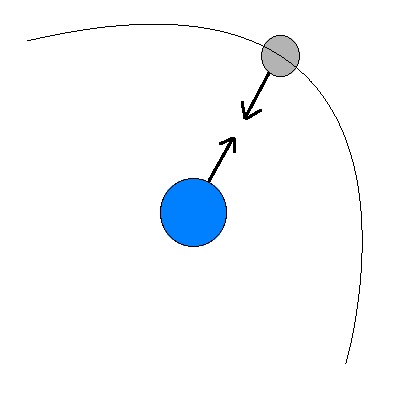
Aufgabe 1) Mondbahn Der Mond bewegt sich mit der Umlaufzeit T = 27,3 d um die Erde. Der Radius der als Kreis um den Erdmittelpunkt angenommenen Mondbahn ist R = 3,84 E5 km a) Bestimmen Sie die Bahngeschwindigkeit v des Mondes auf seiner Kreisbahn. b) Die Gravitationskraft, mit der die Erde den Mond anzieht, wirkt als Zentripetalkraft, die diesen auf die Kreisbahn um die Erde zwingt. Bestimmen Sie über diesen Kraftansatz die Masse der Erde.

Aufgabe 2: Satellit a) Ein Satellit der Masse m umläuft die Erde auf einer Kreisbahn. Bestimmen Sie über einen geeigneten Kraftansatz eine allgemeine Gleichung für die Kreisbahngeschwindigkeit und erläutern Sie, von welchen Größen diese in welcher Art abhängt. b) Berechnen Sie die Kreisbahngeschwindigkeit eines Satelliten, der die Erde knapp über der Erdoberfläche umläuft (d.h. r = Erdradius). c) Berechnen Sie die Höhe über dem Äquator, in der ein Wettersatellit „stehen“ muss, wenn er immer denselben Ausschnitt der Erdoberfläche beobachten soll. Berechnen Sie die Geschwindigkeit eines solchen Satelliten. d) Welche Kreisbahnen sind für Erdsatelliten überhaupt möglich? Erläutern Sie insbesondere, warum ein solcher Satellit nicht ständig über dem 50°-Breitenkreis der Erde fliegen kann.

zurück home inhalt Lösungen