Exponentialfunktionen
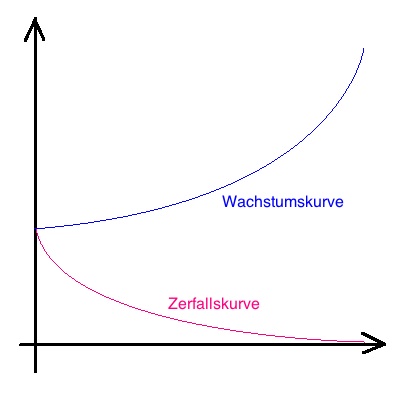
Typische Wachstums- und Zerfallskurven
Grundlagen: natürliche Wachstums- und
Zerfallsprozesse
Viele Prozesse in der Natur basieren auf einem gemeinsamen
mathematischen Prinzip: dem exponentiellen Wachstum bzw. dem
exponentiellen Zerfall.
Beim exponentiellen Wachstum handelt es sich um ein
sich ständig beschleunigendes Wachstum. D.h. je höher ein Wert ist,
desto größer ist der Anstieg der Werte. Beispiele sind das
Bakterienwachstum unter günstigen Bedingungen oder die Erzeugung freier
Neutronen in einer Kernspaltungswaffe.
Beim exponentiellen Zerfall beginnt die Kurve mit
einer starken Abnahme. Die Abnahme wird nun immer schwächer, bis sich
die Kurve langsam immer weiter einem Grundwert (i.d.R. Null) annähert,
diesen aber nie erreicht. Beispiele sind der radioaktive Zerfall, der
Luftdruck in Abhängigkeit von der Höhe oder der Temperaturverlauf in
einer Tasse Tee. |
 |
Anschauliche Realisierung: Potenzfunktion zur Basis
2
Anschaulich lassen sich diese zwei Prinzipien über
Exponentialfunktionen zur Basis 2 realisieren, d.h. durch die
Funktionen
f(x) = W0 2x/X2 oder g(x) =
Wo (1/2)x/X1/2 = Wo
2-x/X1/2
W0 ist dabei der Grundwert, d.h. der Wert für x=0
X2 ist der Verdoppelungswert, d.h. der Wert, bei dem sich
f(x) zum ersten Mal verdoppelt hat.
X1/2 ist entsprechend der Halbwert.
Beispiel: Eine Kultur aus 10 Bakterien soll sich unter idealen
Bedingungen (d.h. genügend Nahrung, Platz und Wärme) vermehren. Unter
diese Bedingungen teilen sich die Zellen alle 2 Stunden. D.h. f(t) = 10
2t/2h
setzt man nun für t = 4h, 6h oder 10h erhält man die entsprechenden
Bakterienanzahlen zu diesen Zeiten. Dies gilt auch, wenn t eine
beliebige reelle Zahl ist. |
 |
e-Funktion Exponentialfunktion zur Eulerschen
Zahl
Zu jeder beliebigen positiven Zahl außer 1 als Basis ist eine
Exponentialfunktion möglich. Am häufigsten wird allerdings die Basis der
Eulerschen Zahl verwendet. Dabei handelt es sich um eine irrationale Zahl die
mit e = 2,718281828459045235... beginnt.
Die besondere Eigenschaft dieser Zahl ist, dass sie sich bei Integration und
Differentiation nicht ändert. D.h. (ex)' = ex und
∫ex dx = ex
Damit bietet sie sich als Lösung jeder Differntialgleichung der Form f' = c f
an. Differntialgleichungen dieser Form sind in der Regel die Grundlagen für
exponentielle Wachstums- und Zerfallsgesetze.
Verdoppelungswert, Halbwert und e-Funktion
Umrechnung mit ln(2)
Zwischen der anschaulichen Form der Exponentialfunktion zur Basis 2 und der
e-Funktion besteht der folgende Zusammenhang:
f(x) = Wo e-x/X mit X = Zerfallskonstante, nach der
W0 auf ca. 37% abgefallen ist.
Der Halbwert ist entsprechend dann X1/2 = ln(2) X
f(x) = Wo ex/X mit X = Wachstumswert, nach der
W0 auf ca. 170% angestiegen ist.
Der Verdoppelungswert ist entsprechend dann X2 = ln(2) X
zurück
home
inhalt
Lösungen

