Herleitung der Zentripetalkraft

Kraft bei einer gleichförmigen Kreisbewegung

Grundlagen: Beschleunigung und Kraft
1) Die Beschleunigung eines Körpers ist definiert als seine Geschwindigkeitsänderung in der Zeit: a = $\raisebox{1ex}{$\mathrm{\Delta v}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{\Delta t}$}\right.$
2) Wirkt auf einen Körper eine Kraft, so wird er beschleunigt: F = m a

Außerdem nutzt man aus, dass für kleine Winkel die Sinusfunktion annähernd eine Ursprungsgerade mit der Steigung 1 ist, d.h. sin(x)≈x für x<5°, dies gilt insbesondere bei einer Grenzwertbildung x→0

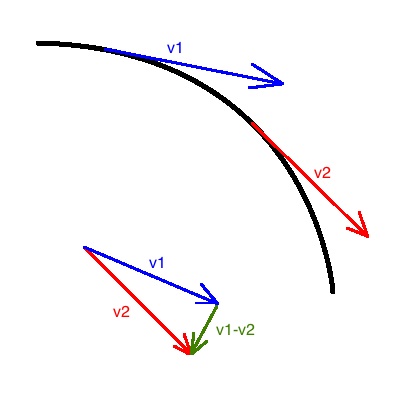
Grundüberlegung: Geschwindigkeitsänderung bei einer Kreisbewegung Bewegt sich ein Körper gleichförmig im Kreis, so ändert sich der Betrag seiner Geschwindigkeit nicht. Aber es ändert sich die Richtung der Geschwindigkeit. Auch diese Geschwindigkeitsänderung muss mit einer Beschleunigung und damit auch mit einer Kraft verbunden sein. Wir erhalten die Geschwindigkeitsänderung durch die Differenz der Geschwindigkeitspfeile. Der zweite Pfeil wurde dabei zum Ansatzpunkt des ersten verschoben.

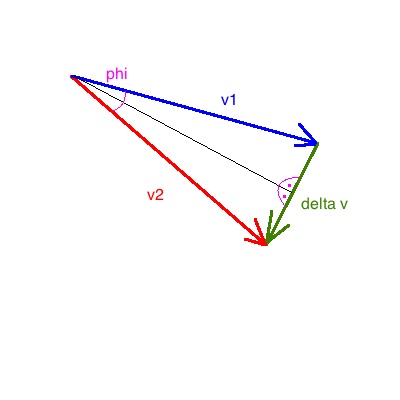
Herleitung: Konstruktion von a aus Δv Da der Betrag der Geschwindigkeit gleich bleiben soll, bildet sich ein gleichschenkliges Dreieck mit den Seitenlängen v1=v2=v und Δv und dem dazwischenliegenden Winkel Δφ. In ihm gilt die Beziehung: sin(1/2 Δφ) = $\frac{1/2\mathrm{\Delta v}}{v}$ Wählen wir den Winkel klein, so können wir vereinfachen: 1/2 Δφ = $\frac{1/2\mathrm{\Delta v}}{v}$ oder Δφ = $\frac{\mathrm{\Delta v}}{v}$ Daraus folgt: Δv = v·Δφ Lassen wir nun den Zeitabstand Δt bliebig klein werden, so erhalten wir einen Grenzwert: $a=\underset{t\to 0}{lim}\frac{\mathrm{\Delta v}}{\mathrm{\Delta t}}=\underset{t\to 0}{lim}v\frac{\mathrm{\Delta \phi }}{\mathrm{\Delta t}}=\mathrm{v\omega }=\mathrm{\omega r\omega }={\omega }^{2}r$ also a = ω2r Mit F = ma erhalten wir für die Zentralkraft: Fz = m ω2 r oder mit ω=v/r: Fz=m v2 / r.

zurück home inhalt