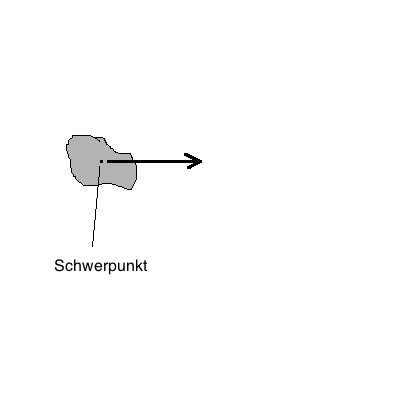
Translation und Rotation im Vergleich

Eine Gegenüberstellung der relevanten Größen

Grundlagen: Der Analogieschluss
Aus der Translation, d.h. der geradlinigen Bewegung kennen wir eine ganze Reihe mächtiger Werkzeuge zur Beschreibung dieser Bewegung.
Diese Gleichungen lassen sich durch Neudefinition der Basisgrößen auf die Rotation, d.h. auf die Drehung um eine feste Achse übertragen.

Die folgende Tabelle stellt alle Größen und Gleichungen sowie die Umrechnungsprozeduren dar.

Analogie zwischen Translation und Rotation

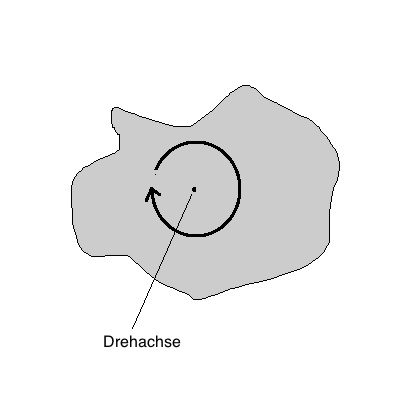
Translation	Umrechnung	Rotation
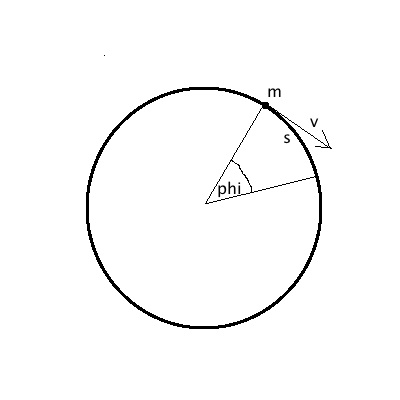
Strecke s s = ${\int }_0^{t}v\mathrm{dt}$	s = φ r mit r:Radius	Drehwinkel φ im Bogenmaß φ = ${\int }_0^t\omega$dt
Geschwindigkeit $v=\frac{\mathrm{\Delta s}}{\mathrm{\Delta t}}$	v = ω r	Winkelgeschwindigkeit $\omega =\frac{\mathrm{\Delta \phi }}{\mathrm{\Delta t}}$
Beschleunigung $a=\frac{\mathrm{\Delta v}}{\mathrm{\Delta t}}$	a = α r	Winkelbeschleunigung $\alpha =\frac{\mathrm{\Delta \omega }}{\mathrm{\Delta t}}$
Bewegungsgleichung der Translation: s = 1/2 a t2	-	Bewegungsgleichung der Rotation: φ = 1/2 α t2
Geschwindigkeitsgleichung der Translation: v = a t	-	Geschwindigkeitsgleichung der Rotation: ω = α t
Masse m	Für eine Masse auf einer leichten Drehachse oder einen dünnwandigen Hohlzylinder gilt: J = m r2 Für andere Körper existieren entsprechend andere Gleichungen.	Trägheitsmoment J
Kraft F Es gilt das 3. Newtonsche Axiom F = m a	M = F r, wenn F senkrecht r sonst gilt: M = F r sin(β) mit β: Winkel zwischen F und r oder M = F ⊗ r	Drehmoment M Es gilt: M = J α
kinetische Energie W = 1/2 m v2	-	Rotationsenergie W = 1/2 J ω2
Impuls p = m v	L = p ⊗ r	Drehimpuls L = J ω

zurück home inhalt