Die Bewegungsgleichung der Rotation

Ein Experiment zur Bestimmung des Trägheitsmomentes

Grundlagen: Die Bewegungsgleichung der Rotation
Die Bewegungsgleichung der Translation (geradlinigen Bewegung) lautet:
s=1/2 a t² mit s:Strecke, a: Beschleunigung, t: Zeit
Die Beschleunigung erfolgt durch eine Kraft, für die gilt:
F = m a mit F: Kraft, m: Masse

Durch Analogieschluss erhält man strukturell gleiche Formeln für die Drehbewegung:
φ=1/2 α t² mit φ: Drehwinkel, α: Winkelbeschleunigung t: Zeit
M = J α mit M: Drehmoment, J: Trägheitsmoment

Das Drehmoment ist (z.B. aus dem Hebelgesetz heraus) definiert als :
M = F r mit F: wirkende Kraft, r: Abstand zur Drehachse
Diese Gleichung gilt aber nur, wenn F und r senkrecht aufeinander stehen.

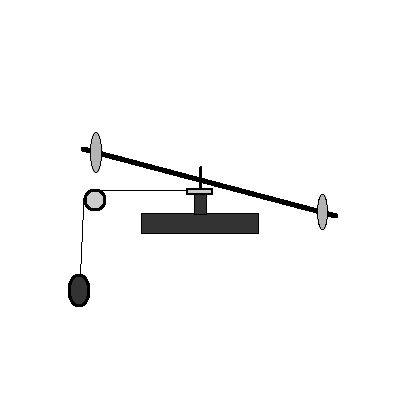
Versuch: Schwungachse Über den nebenstehenden Versuch kann man unter Zuhilfenahme der Bewegungsgleichung das Trägkeitsmoment bestimmen. Gehen Sie wie folgt vor: - Bestimmen Sie aus der Gewichtskraft der angehängten Masse und dem Radius des Angriffspunktes des Fadens am Drehgestell das wirkende Drehmoment M. - Messen Sie nun die Zeit für mehrere Umläufe der Drehachse und bestimmen Sie aus der Bewegungsgleichung die wirkende Winkelbeschleunigung α. - Schließlich können Sie über die Gleichung M = J α das Trägkeitsmoment bestimmen. - Prüfen Sie anschließend, ob dieser Wert mit dem theoretischen Wert übereinstimmt. Wiederholen Sie die Messung für - verschiedene Drehmomente und - verschiedene Trägheitsmomente.

zurück home inhalt Lösungen