Geschwindigkeitsmessungen mit einem Wagen

Gleichförmige und beschleunigte Bewegungen und ihre Darstellung in s-t-Diagrammen.

Grundlagen: Geschwindigkeit und Beschleunigung

Die Geschwindigkeit ist definiert als das Verhältnis von zurückgelegter Strecke zu der dafür benötigten Zeit. v = s/t
Für die Momentangeschwindigkeit muss jeweils die Differenz zu den vorhergehenden Strecken- und Zeitwerten berechnet werden, bevor der Quotient gebildet wird. D.h. die Gleichung lautet v = Δs/Δt

Von einer Beschleunigung spricht man, wenn sich die Geschwindigkeit ändert. Dies gilt sowohl für das eigentliche Beschleunigen d.h. scneller werden (positive Beschleunigung) als auch für das Abbremsen (negative Beschleunigung). Sie ist definiert alsdas Verhältnis von Geschwindigkeitsänderung und der dafür benötigten Zeit. a = v/t
In der Regel ist die momentane Beschleunigung gemeint, wenn man von einer Beschleunigung redet. D.h. zur Berechnung der Beschleunigung darf man nicht einfach den Geschwindigkeitswert durch die Zeit teilen, sondern man muss jeweils die Differenz zum vorherigen Wert bilden. Es gilt also : a = Δv/Δt

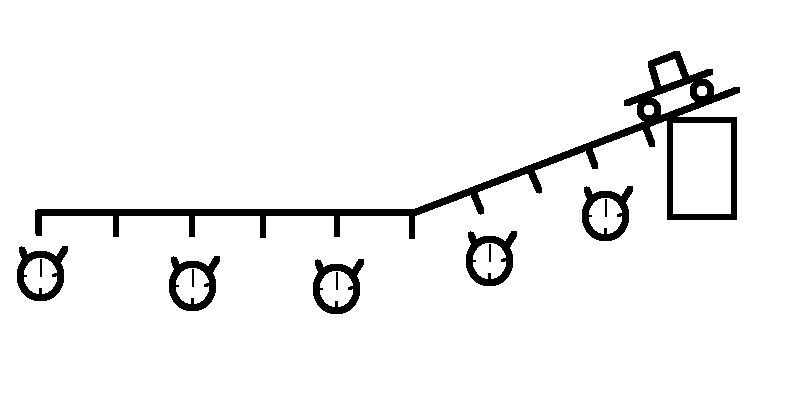
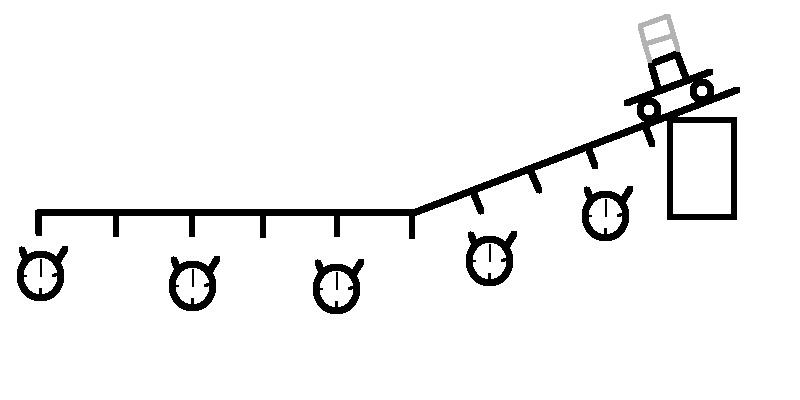
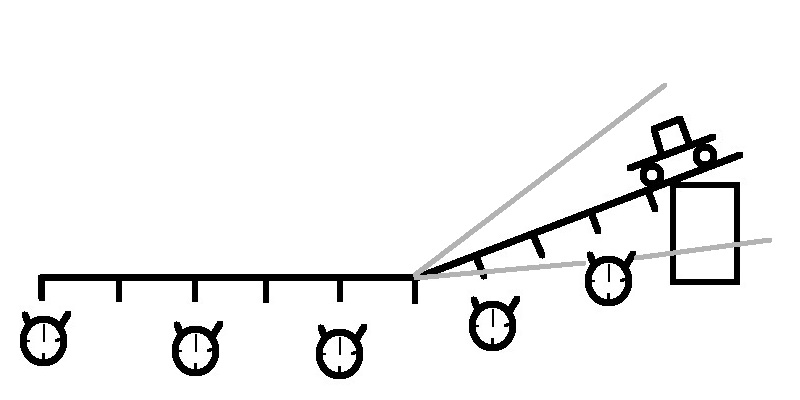
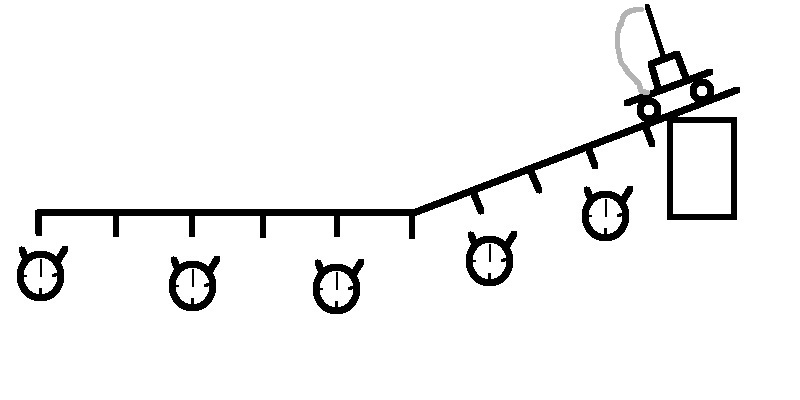
Messung mit einem Wagen Aus zwei Schienen wird die Messstrecke zusammengesetzt. Unter die erste Schiene wird auf der einen Seite ein Klotz untergelegt, damit die Schiene schräg steht. Die zweite Schiene wird bündig an dei erste angefügt und liegt flach auf dem Tisch. Nun wird in gleichmäßigen Abständen (z.B. alle 10 cm) eine Markierung auf den Schienen aufgebracht. Der Wagen wird nun mehrmals die Schienenkombination hinuntergerollt und für jede Markierung wird die Zeit gemessen. Dabei können pro Durchgang je nach Gruppengröße mehrere Messungen stattfinden. 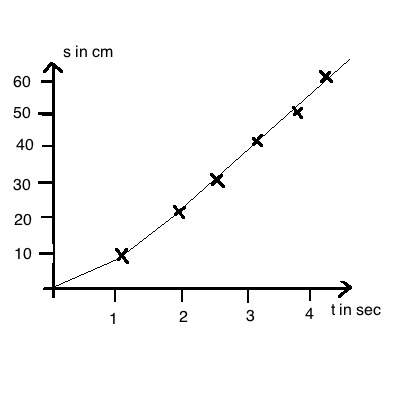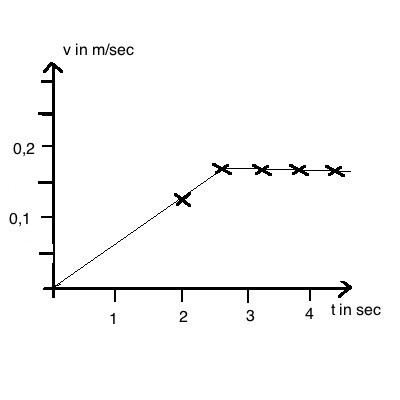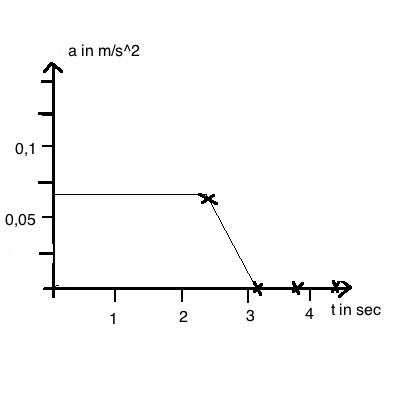Die Messwerte werden in der unten stehenden Weise ausgewertet.

Qualitative Beschreibung
Beschreibe die Bewegung des Wagens in eigenen Worten.

Auswertung der Messwerte Trage die gemessenen Zeiten und Strecken in die nebenstehende Tabelle (Beispiel!) ein. Berechne die Momentangeschwindigkeiten, indem Du zunächst für Zeit und Strecke die Differenz zum vorhergehenden Wert bildest und erst dann teilst. Natürlich gibt es für die erste Spalte keinen Wert, da die erste Spalte keinen Vorgänger hat. Aus den Momentangeschwindigkeiten können dann die Beschleunigungen (s.o.) berechnet werden.

s in cm 10 20 30 Schienenwechsel 40 50 60 t in sec 1,2 2,0 2,6 Schienenwechsel 3,2 3,8 4,4 Momentangeschwindigkeit in m/s --- 0,125 0,166 Schienenwechsel 0,166 0,166 0,166 Beschleunigung in m/s2 --- --- 0,068 Schienenwechsel 0 0 0

Auswertung im Diagramm Die Messwerte und die berechneten Geschwindigkeiten und Beschleunigungen werden nun grafisch dargestellt. Traditionell wird die Zeit immer auf der waagerechten Achse aufgetragen, so dass s-t-, v-t- und a-t-Diagramme entstehen. Anschließend werden die Diagramme verglichen und die Bedeutung ihres Verlaufs erörtert.

Messalternative 1) Die Messung wird wiederholt, allerdings verändert man dabei die Masse des Wagens, indem man verschiedene Massestücke auflegt. Für das überraschende Ergebnis reicht es aus, zwei sehr verschiedene Massen aufzulegen.

Messalternative 2) Die Messung wird wiederholt, allerdings verändert man dabei die Neigung der ersten Bahn, indem man verschiedene Klötze unter die linke Seite legt.

Messalternative 3) Die Messung wird wiederholt, allerdings erhält der Wagen ein möglichst großes Segel aus Papier, so dass er auf der waagerechten Strecke abbremst .

zurück home inhalt Lösungen