| Aufgabe 1) Graphen
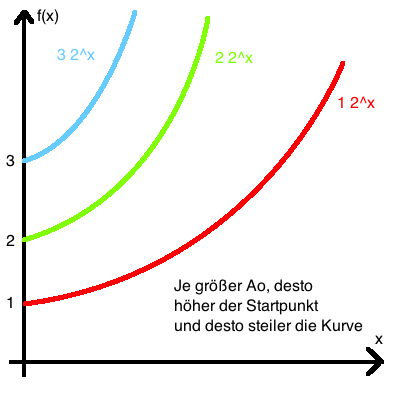
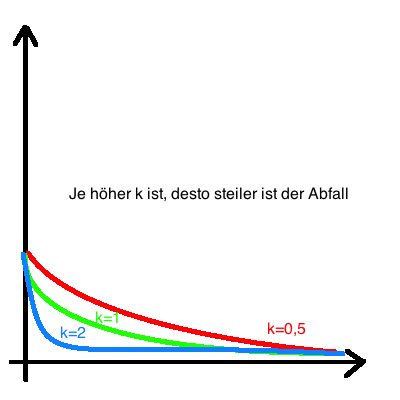
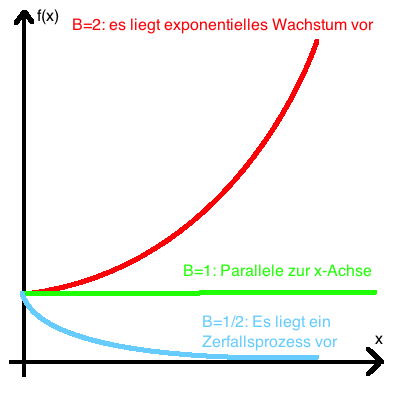
Es sollten folgende Graphen entstehen: |

|
f(x) = A0 Bkx
Umstellung nach A0:
Teilen durch Bkx
A0 = f(x)/Bkx
Umstellen nach k:
Teilen durch A0, dann Logarithmus auf beiden Seiten nehmen, Logarithmusgesetz anwenden und schließlich durch x und ln(B) teilen:
f(x)/A0 = Bkx
ln(f(x)/A0) = ln(Bkx)
ln(f(x)/A0) = kx ln(B)
k = ln(f(x)/A0)/ (x ln(B))
Umsetellen nach x:
Wie nach x, nur zum Schluss durch k statt durch x teilen:
x = ln(f(x)/A0)/ (k ln(B))
Es werden nur die Ergebnisse angezeigt.
a)
N0 = N(t)/(1/2)t/T1/2
N0 = N(t)/e-ln(2)t/T1/2
t = ln(N(t)/N0) / ln(1/2) * T1/2
t = - ln(N(t)/N0) / ln(2) * T1/2
T1/2 = ln(1/2) t / ln(N(t)/N0)
T1/2 = - ln(2) t / ln(N(t)/N0)
b)
U0 = U(t)/(1/2)t/ln(2)RC
U0 = U(t)/e-t/RC
t = ln(U(t)/U0) / ln(1/2) * ln(2)RC
t = - ln(U(t)/U0) RC
R = ln(1/2) t / C ln(U(t)/U0)
R = - t / C ln(U(t)/U0)
C = ln(1/2) t / R ln(U(t)/U0)
C = - t / R ln(U(t)/U0)
