LÖSUNG m-0017

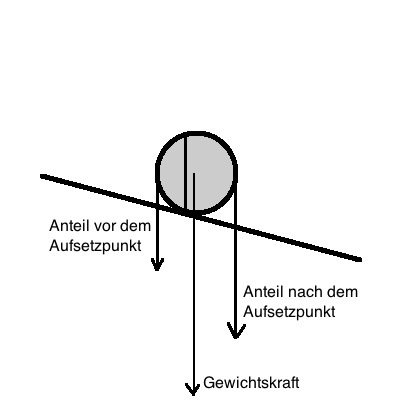
Aufgabe: Wettrennen der Formen a) Skizze nebenstehend Argumentation für das Drehmoment: Der Aufsetzpunkt für alle Körper befindet sich nicht unter sondern vor dem Schwerpunkt. Damit wirkt vor dem Aufsetzpunkt eine geringere Masse als dahinter. Somit überwiegt der Anteil der Schwerkraft hinter dem Aufsetzpunkt und es kommt zu einem Drehmoment.

b) Der Hohlzylinder hat offenbar bei gleicher Masse und gleichem Radius das größte Trägheitsmoment, die Vollkugel das kleinste.
Daraus folgt die Reihenfolge: Vollkugel - Vollzylinder - Hohlkugel - Hohlzylinder für die Ankunftszeiten.

c) m g h = 1/2 m v² + 1/2 J ω² = = 1/2 m v² + 1/2 m R² v² / R² für den Hohlzylinder= m v ²
Die Ergebnisse im Einzelnen lauten:
Hohlzylinder: v= $\sqrt{gh}$ = 1,085 m/s
Vollzylinder: v = $\sqrt{\frac{4}{3}gh}$= 1,253 m/s
Hohlkugel: v= $\sqrt{\frac{3}{2}gh}$= 1,329 m/s
Vollkugel: v= $\sqrt{\frac{10}{9}gh}$= 1,297 m/s

d)
Berechnung von W_kin=1/2 m v² und W_rot= 1/2 J ω² und Vergleich mit W_ges = mgh = 2,3544 J
Ergebnisse:

	Wkin in %	Wrot in %
Hohlzylinder	50	50
Vollzylinder	66,63	33,33
Hohlkugel	60	40
Vollkugel	71,43	28,57

e) Es gelte s = 1/2 a t² und v = at sofern v₀=0 und s₀=0
Ineinander einsetzen ergibt
s = 1/2 v t
Damit folgen die Abrollzeiten zu
t = 2s/v

t_HZ= 4,6 sec
t_VZ= 4,0 sec
t_HK= 4,2 sec
t_VK= 3,86 sec
Die Vermutung aus b) wurde also bestätigt.

f) Es gelten:
v = a t => a = v/t
ω = J α => α = ω/J
und
F = m a
M = J α

Damit ergeben sich folgende Werte:

	a in m/s2	α in s2	F in N	M in Nm
Hohlzylinder	0,24	4.300	0,47	21,7
Vollzylinder	0,31	10.000	0,63	25
Hohlkugel	0,28	7.100	0,57	23,8
Vollkugel	0,38	13.000	0,67	26

zurück home inhalt