Lösung e-0074

Schritt 1) Reiben des Stabes: Beim Reiben des Stabes Lösen sich Elektronen aus dem Fell und gehen in den Stab über. Der Stab ist nun negativ geladen, das Fell positiv.
Begründung: Die Elektronen sind im Kunststoff stärker gebunden als im Fell.

Abstreifen des Stabes am Elektroskop: Die überschüssigen Elektronen des Stabes gehen solange auf das Elektroskop über und verteilen sich dort, bis beide gleich stark geladen sind.
Begründung: Der Ladungsausgleich erfolgt so schnell, dass ein ausgeglichener Zustand erreicht wird.

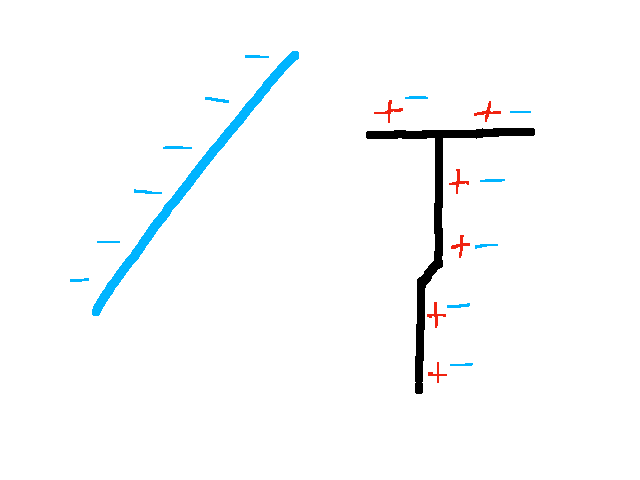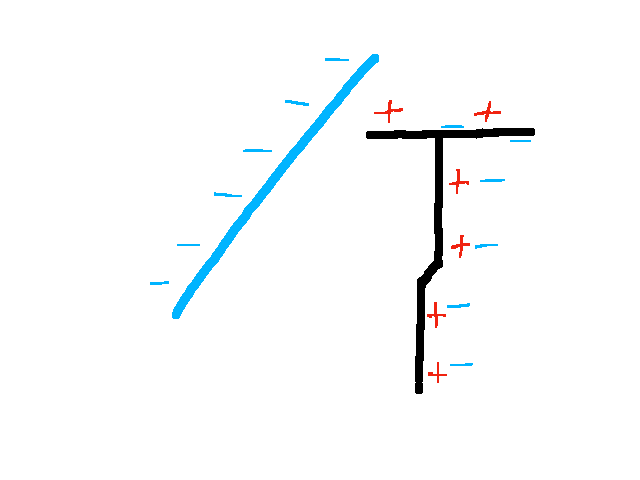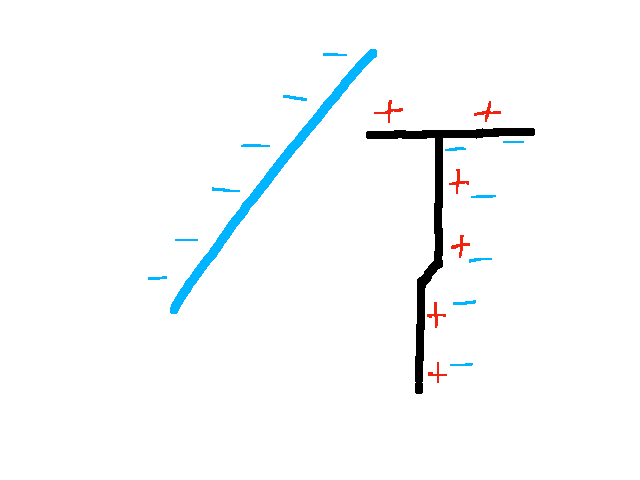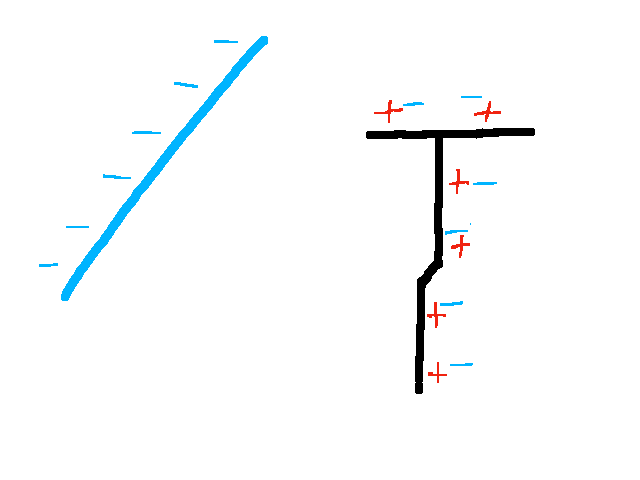
Wird der negativ geladene Stab an das Elektroskop angenähert, so verdrängt die negative Ladung des Stabes die Elektronen im Elektroskop in den Stab. Dieser ist wie auch der Zeiger negativ geladen und der Zeiger schlägt aus.
Wird der Stab wieder entfernt, so kehren die Elektronen wieder in die ursprüngliche Position zurück und das Elektroskop ist wieder überall neutral geladen.

Um die Anzahl der bewegten Elektronen zu erhalten, benötigen wir die Ladung eines einzelnen Elektrons, die Elementarladung e.
geg.: e=1,6E-19C Q=6E-6C
ges.: N
Ansatz: N=Q/e = 6E-6C/1,6E-19C = 3,75E13

Nun benötigen wir die Anzahl der Im Eisen enthaltenen Elektronen. Dazu berechnen wir zunächst die Masse eines Eisenatoms aus seiner Massenzahl, dann die Anzahl der Eisenatome in der Masse von 60g und schließlich die Anzahl der Elektronen aus der Ordnungszahl.
Die Masse eines Eisenatoms erhalten wir aus der Massenzahl und der Atomaren Masseneinheit u zu:
m_Fe=55,85 u = 9,2711E-26 kg
Damit erhalten wir die Anzahl der im Elektroskop enthaltenen Eisenatome zu:
N=m/m_Fe=0,06kg/9,2711E-26 kg = 6,472 E23
Damit erhalten wir über die Ordnungszahl die Anzahl der Elektronen zu:
N_e=N 26 = 1,683 E25
Der relative Anteil der bewegten Elektronen ist damit:
A = 3,75 E13 / 1,683 E25 = 2,23 E-12
Dieser Anteil ist also sehr gering, es wird gerade einmal jedes billionste Elektron bewegt.

Strom ist bewegte Ladung. Es gilt also: I = Q/t
Damit erhalten wir einen Strom von:
I = 6E-6C / 1E-3s = 6 mA

Für die Berechnung der abgefallenen Spannung benötigen wir das Ohmsche Gesetz:
U = R I = 1600 Ohm 6mA = 9,6 V
Die mittlere Leistung beträgt dann.
P = U I = 9,6V 6mA = 57,6 mW
Die umgesetzte Energie erhalten wir aus:
W = P t = 57,6 mW 1 ms = 57,6 E-6 J