a) gegeben: L = 4mH = 0,004H; C = 80&mikro;F = 80E-6. F = 0,000.08F
gesucht: f0
Ansatz: Für die Eigenfrequenz einer Reihenschaltung gilt:
f0 = 1/(2πWurzel(LC)) = 281,35Hz
b) Der ohmsche Widerstand bleibt unverändert, d.h. er hat einen Wert von 10Ω, 30Ω oder 70Ω.
Für den Widerstand des Kondensators gilt:
RC= 1/ωC = 1/(2πfC) =7,07Ω
Für die Spule gilt: RL= ωL = 2 πfL = 7,07Ω
Die Widerstände von Spule und Kondensator sind also gleich!
Gesamtwiderstand ohne Rechnung: Bei der Eigenfrequenz heben sich die Widerstände von Kondensator und Spule auf. Es bleibt also nur der ohmsche Widerstand von 10Ω, 30Ω oder 70Ω übrig.
| c) Für jeden ohmschen Widerstand muss der Gesamtwiderstand nach folgender Gleichung berechnet werden: Rges=Wurzel(Rohm2+(RC-RL)2) Setzt man die Gleichungen für RL und RC in diese Gleichung ein, so folgt: Rges=Wurzel(Rohm2+(1/(2πfC)-2πfL)2) Es ergeben sich folgende Werte: |
|
Je höher der ohmsche Widerstand ist, desto höher liegt der Extremwert der Kurve. Außerdem wird die Kurve flacher.

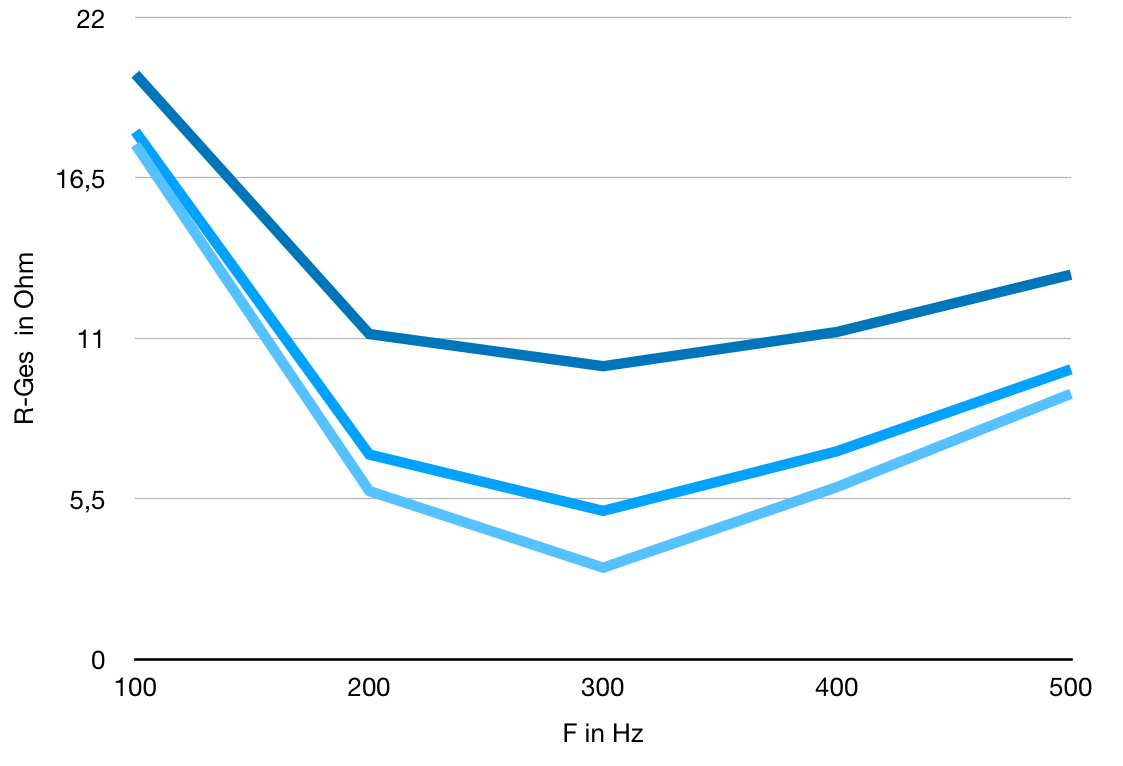
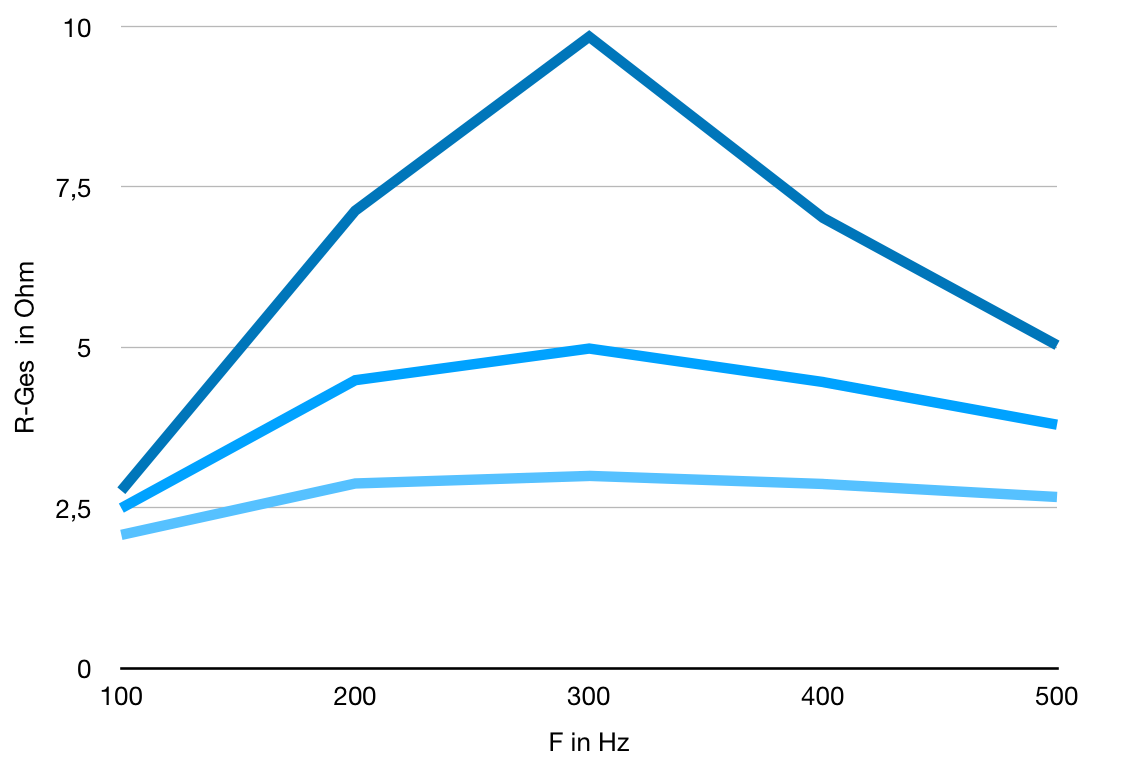 d) Diagramm f über Rges
d) Diagramm f über Rges