Lösung G-0019

Aufgabe

a)Zwischen Erde und Mond entsteht in der Nähe von P ein Punkt, an dem sich die Gravitationskräfte aufheben.

b) Berechnung der Gravitation durch die einzelnen Planeten:
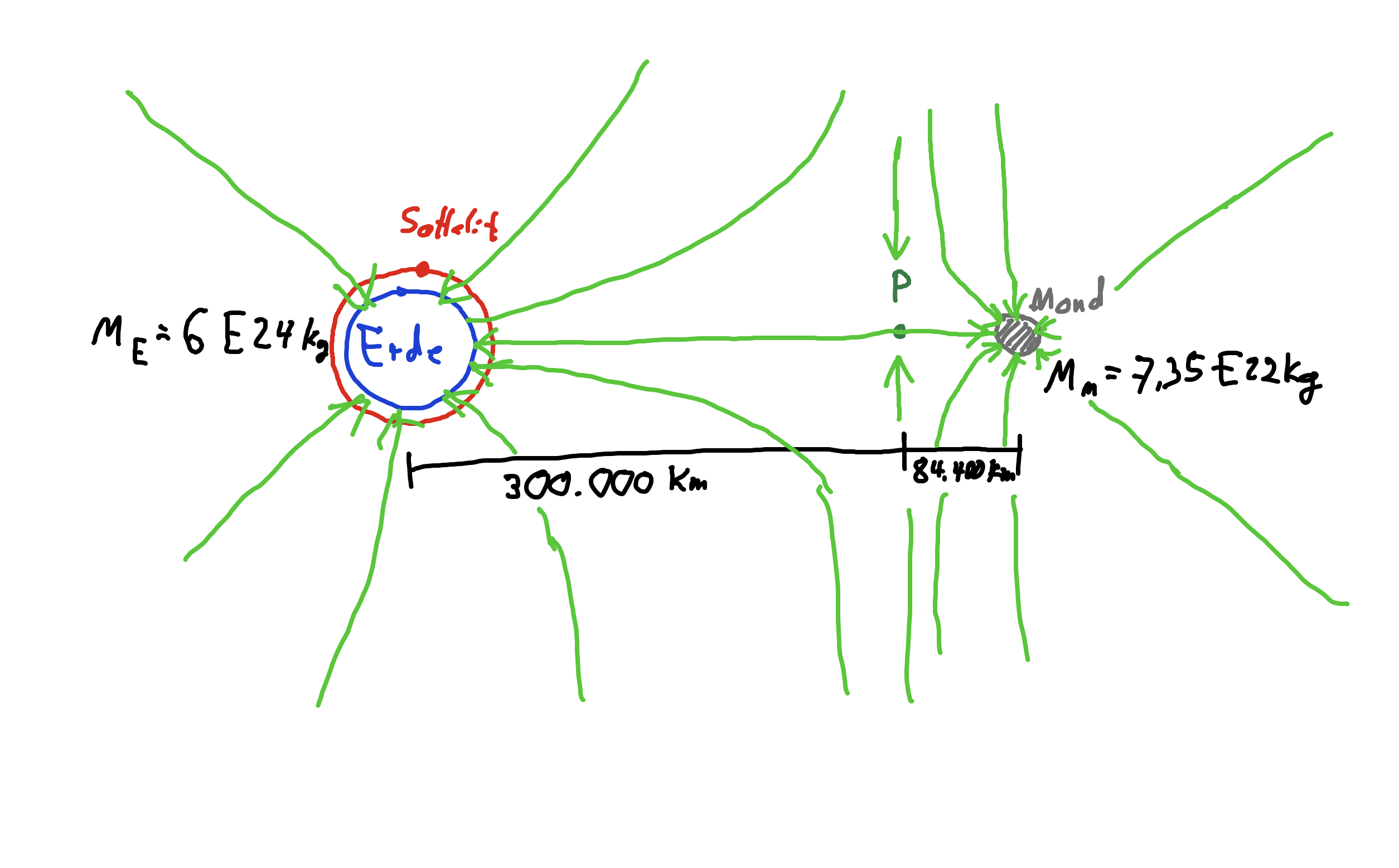
F_{Erde bei 300.000km} = G mM/r² = 0,0089N
entsprechend: F_Mond = 0,0014 N
Die Kräfte heben sich zum Teil auf:
F_g = 0,0089N-0,0014N = 0,0075N

c) Die Gravitationskraft wirkt als Zentripetalkraft:
G mM/r² = m (2π/T)²r
=> T = 2πWurzel(r³/MG) = 6.031,3s entspricht ca. 100min oder knapp 2 h.

d) Bewegt sich der Satellit auf den Mond zu, so beschleunigt er. Bewegt er sich vom Mont weg, so wird er langsamer. Dadurch befindet sich der Satellit zwischen Mond und Erde näher am Mond während er hinter der Erde näher an der Erdoberfläche ist.

e) Der Satellit verlässt den Einfluss der Erde, wenn die kinetische Energie die potentielle Energie des Gravitationsfeldes verlässt.
W_kin > W_pot
1/2 m v² = G mM / r
=> v = Wurzel(2GM/r) = 10.564,9 m/s

f) Der Satellit bewegt sich auf einer Ellipsenbahn, in deren einem Brennpunkt der Erdmittelpunkt liegt. Dabei verliert er Geschwindigkeit, wenn er sich von der Erde entfernt und gewinnt sie bei Annäherung.
Der Fahrstrahl zwischen Erdmittelpunkt und Satellit überstreicht dabei in gleichen Zeiten gleiche Flächen.

g) Das 3. Kepplersche Gesetz lautet:
T₁²/T₂² = R₁³/R₂³,
wobei R₁ der Radius der Mondbahn (384.000km) und R₂ der Bahnradius des Satelliten (6371km + 800 km) ist.
T₂ kennen wir aus Aufgabe c).
=> T₁ = Wurzel(T₂² * R₁³/R₂³) = 2.366.565 s = 27,4 d was etwa einem Monat entspricht...