Lösung: G-0017

Aufgabe 1)

a) Die Gewichtskraft an der Erdoberfläche ist:
F_g = m g = 2,2563 N
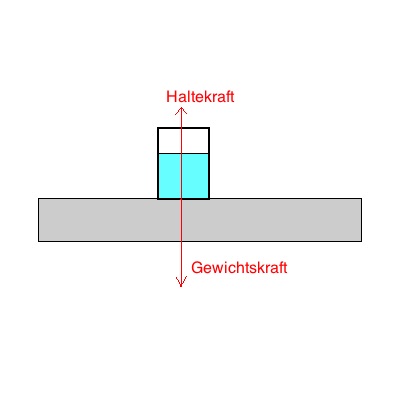
Zeichnung nebenstehend, Die Pfeile sollten beide 2,26cm lang sein.

b) 1. Gesetz: Die Kräfte heben sich auf, daher bleibt der Becher in Ruhe
3. Gesetz: actio = reactio: Die Gewichtskraft erzeugt eine gleich große Haltekraft des Tisches.

c) Wir können die Gewichtskraft an der Erdoberfläche auf zwei Arten berechnen:
F_g = mg und
F_G= G mM_E/R_E² mit M_E: Erdmasse;R_E: Erdradius
Ein Vergleich dieser beiden Gleichungen liefert:
GM_E/R_E² = g
Setzt man die Werte der Erdmasse, des Erdradius und der Gravitationskonstanten ein, so erhält man g = 9,81 m/s²

d) Zunächst benötigen wir die Geschwindigkeit, mit der sich ein Objekt am Äquator um die Erde bewegt.
Diese erhalten wir aus dem Erdumfang (U_E = 2 π R_E= 40.000km) und einer Tageslänge (T = 24*60*60 s)
Damit erhalten wir: v = U_E/T = 2πR_E/T = 462,4 m/s
Damit erhalten wir die für diese Bewegung nötige Zentripetalkraft:
F_z = m v²/R_E = 0,007733581 N
Vergleicht man diesen Wert mit der Gewichtskraft
F_g = m g ,
so ergibt dies 0,343 % der Gewichtskraft.

e) Wir müssen den größer gewordenen Radius in der Newtonschen Gravitationsgleichung berücksichtigen:
F_g' = G $\frac{m M_{E}}{{(R_{E} + 8848 m)}^{2}}$ = 2,25 1 N
Vergleicht man dies mit der Gewichtskraft
F_g= m g,
so weicht dieser Wert um dF = 0,0062 N
oder 0,275 % von der Gewichtskraft an der Erdoberfläche ab.

Aufgabe 2)
a) Die Gewichtskraft wirkt als Zentripetalkraft:
mω²r = G mM/r²
Wir lösen nach r auf:
=> r³ = GM/(2π/T)² => r = 42.170 km
Für die Höhe müssen wir noch den Erdradius abziehen:
h = r-R_E = 35811 km
b) Als geostationärer Satellit soll er einmal am Tag um die Erde kreisen.
mit T = 1d = 24*60*60 s und r aus Aufgabe a) erhalten wir:
v = 2πr/T = 3002 m/s
Die kinetische Energie ist damit:
W_kin = 1/2 m v² = 940,43 MJ
Für die potentielle Energie im Gravitationsfeld gilt:
W_pot = GMm(1/R_E²-1/r²) = 10,6 GJ
Die Hauptenergie muss für das Heben, nicht für die Beschleunigung aufgebracht werden.

Aufgabe 3)
a) Wir berechnen beide Seiten des Kepplerschen Gesetzes:
T_S² / T_M² = 1d²/27,5d² = 0,001322
R_S³ / R_M³ = 0,0011717
Die Werte sind annähernd gleich.
b) Ansatz: Die Gravitationskraft wirkt als Zentripetalkraft:
F_g = F_z oder
$G \frac{mM}{r^{2}} = m ω^{2} r = m \frac{4 π^{2} r}{T^{2}}$
Wir lösen nach r auf:
=> $r^{3} = G \frac{M T^{2}}{4 π^{2}}$ = $\frac{GM}{4 π^{2}} T^{2}$ = C T² mit C = GM/4π²
D.h. dass T² proportional zu R³ ist.
c) Wir beginnen mit dem Ansatz aus b) und lösen nach M auf:
M = r³ / T² 4π²/G = 6,7 E24 kg (Rechnung mit den Werten für den Mond) oder 5,94 E24 kg (Rechnung mit den Werten für den geostationären Satelliten)

zurück home inhalt