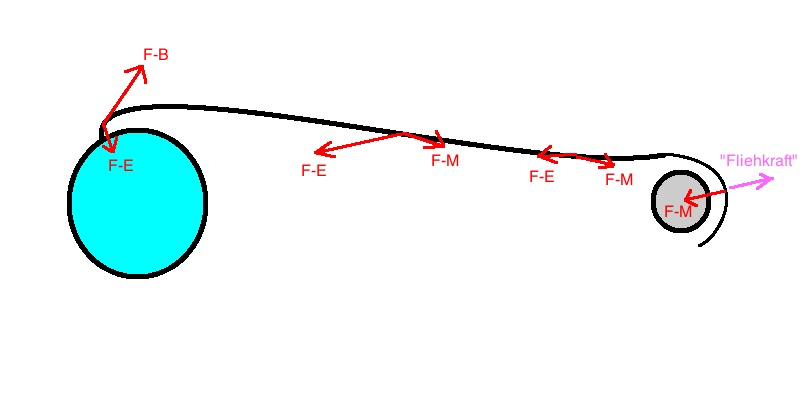
In der Beschleunigungsphase muss Fg < FB sein.
Am in c) berechneten Umkehrpunkt müssen FE und FM gleich groß sein.
Am Mittelpunkt gilt FE > FM
In der Umlaufbahn wirkt eigentlich nur FM, die andere Kraft ist eine Scheinkraft.
Fingerübung Gravitation
Aufgabe 1)
a) mg = G mME/RE2
=> RE = = 6358 km
[R] = 1=1 m
gM = G MM / RM2 = 1,624
m/s2
[g] =1 =1 m/s2
b) Es gilt das Gravitationsgesetz: Fg=
G
Für die Gravitationskraft der Erde bei 200.000km gilt damit: FE =
57,5N
Entsprechend gilt für die Gravitationskraft des Mondes: FM = 0,711
N
=> Fres = FE-FM = 56,792 N
c) FE = FM also
<=>
=>
oder 0 = x2 + p x + q mit p =
und q =
Durch Anwenden der p-q-Formel folgt:
x = 359.965,8 km
Die zweite Lösung liegt hinter dem Mond.
d) Die Gravitationskraft des Mondes wirke als Zentripetalkraft.
m v2 / r = G m MM/r2
=> v = = 1624,8 m/s
T = U/v = 2πr/v = 7184,8sec = 1,996 h
e)
| Phase | Axiom | Begründung |
| Start | actio = reactio | Die Triebwerke drücken den Treibstoff nach unten während die Rakete nach oben gedrückt wird. |
| Beschleunigungsphase | zusätzlich: F = ma | Die Triebwerke beschleunigen die Rakete. |
| nach Abschaltung der Triebwerke | innerhalb der Kapsel: Newton 1 | Es herrscht scheinbar Schwerelosigkeit und damit völlige Kräftefreiheit. |
| von Außen betrachtet: F = m a | Die Gravitationskräfte von Erde und Mond bremsen und beschleunigen die Kapsel. | |
| Abbremsen | wie Beschleunigungsphase | |
| Umlaufbahn | von Außen betrachtet: F = m a und nicht (!) actio = reactio oder Newton 1 | Die Gravitationskraft des Mondes wirkt als Zentripetalkraft und beschluenigt die Kapsel durch Richtungsänderung, obwohl sich der Betrag der Geschwindigkeit nicht ändert. |
| Innerhalb der Kapsel Newton 1 | Die Gravitationskraft des Mondes und die Zentrifugalkraft (Scheinkraft !) heben sich gegenseitig auf. |
Aufgabe 2)
a) Für das Gravitationspotential gilt: W =
dW = WErdoberfläche - W(359.966 km) für Erde UND Mond!
=> W = ( - ) -( - ) = 3,5 E11 J
b) Für die Umlaufbahn gilt:
Wpot = - = 1,1 E10 J
Außerdem gilt:
Fg = Fz und somit
v = = 7776,3 m/s und somit Wkin = 1/2 m v2 = 1,75 E11
J
=> Wges = 1,864 E11 J was 53% der Energie aus a) entspricht.
c) Die Kapsel muss mindestens die Potentielle Energie des Mondes abzüglich der
potentiellen Energie der Erde aufnehmen, bis sie 120km über der Mondoberfläche
ist.
Somit gilt:
dW = ( - ) - ( - )
= 3,22 E9 J
Wandelt sich diese Energie vollständig in kinetische Energie um, so folgt:
v = = 1054 m/s
Dieser Wert liegt unterhalb der benötigten Geschwindigkeit (siehe 1d) ). Die
Kapsel würde also ohne Beschleunigung abstürzen!
Aufgabe 3) Kepplersche Gesetze
a) Ansatz: Fg = Fz oder
=> == 1,0045 E13 m3
b) Aus v=7776,3 m/s und R = RE + 200 km folgt
T = 2πR/v = 5299sec = 1,472h
und mit den Daten des Mondes:
= 4,9 E-6 und = 4,4 E-6