Lösung: G-0002

Aufgaben zum Gravitationsgesetz

Aufgabe 1) Cavendish-Versuch
a) Das Gravitationsgesetz lautet:
F_G=G$\frac{\mathrm{mM}}{r^2}$=6,67E-11m³/kg s²$\frac{1\mathrm{kg}\mathrm{0,1}\mathrm{kg}}{{\left(\mathrm{0,05}m\right)}^2}$= 2,66971E-9 N
b) Verdoppelt man eine Masse, verdoppelt sich auch die Kraft.
Verdoppelt man beide Massen, vervierfacht sich die Kraft.
Verdoppelt man den Abstand, viertelt sich die Kraft.
c) Über die Bewegung der kleineren Kugeln kann die Beschleunigung derselben an den verschiedenen Orten und damit die wirkende Kraft ermittelt werden. Hat man diese bestimmt, so stellt man das Gravitationsgesetz nach der Konstante um und erhält:
G = $\frac{F_G{r}^2}{\mathrm{mM}}$
Durch sehr aufwändige Messungen ist G heute auf 6 Stellen genau bekannt.


Aufgabe 2) Entfernung von der Erde
a) Das Newtonsche Gravitationsgesetz lautet:
F_G=G$\frac{\mathrm{mM}}{r^2}$
Damit ergeben sich bei einer Masse von 3kg für die verschiedenen Entfernungen:
10000km: 11,96N
100000km: 0,1196N
1000000km: 0,001196N
Verzehnfacht sich der Abstand, so wird die Gewichtskraft durch 100 geteilt.

b) Die Gewichtskraft sei 0,5 m g.
Mit dem Newtonschen Gravitationsgesetz ergibt sich somit:
0,5 m g = G$\frac{\mathrm{mM}}{r^2}$
=> r = $\sqrt{\frac{\mathrm{GM}}{\mathrm{0,5}g}}$

r = 9009,9 km
Für die Höhe müssen wir noch den Erdradius abziehen:
h = r-R = 2638,9 km

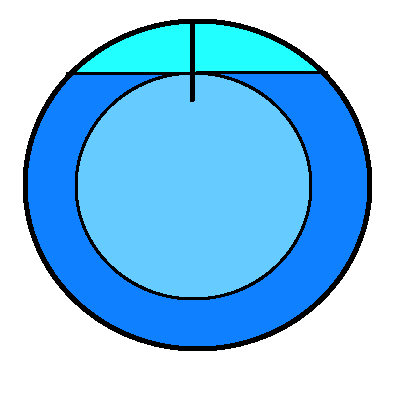
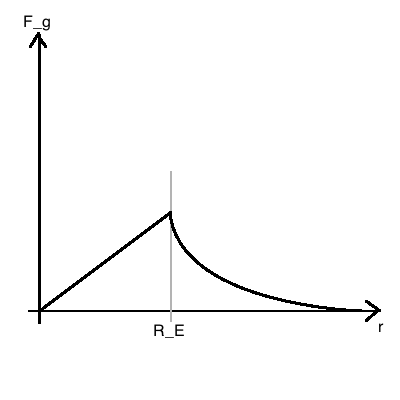
c) Unter der Erdoberfläche ist nur noch der Anteil der Erdmasse relevant, der einen kleineren Radius hat als der Beobachter. Wenn wir eine konstante Dichte σ der Erde annehmen gilt: Mrelevant = σVolKugel = σ 4/3 π r3 Damit ergibt sich für die Gravitationskraft: FG=G$\frac{\mathrm{mM}}{r^2}$=G$\frac{\mathrm{m\sigma }\frac{4}{3}{\mathrm{\pi r}}^3}{r^2}$=G m 4/3 π r Die Gravitationskraft sinkt also linear zum Erdmittelpunkt hin! Da die Gravitationskraft linear abnimmt entspricht die prozentuale Abnahme dem Verhältnis der Tiefe zum Erdradius: 1m: 0,0000157% 1km:0,0157 % 10km:0,157% 100km:1,57% 1000km:15,7%

Aufgabe 3) Ortsfaktoren
a) An der Erdoberfläche sollen beide Gravitationsgesetze gleichwertig gelten:
mg =G$\frac{\mathrm{mM}}{r^2}$
Damit enthält der Ortsfaktor g folgende Elemente:
g =G$\frac{M}{r^2}$ und ergibt g = 9,8225 m/s²
b) Mit dem Ansatz aus a) ergibt sich:
M = g R²/ G
=> M = 1,9 E27 kg

c) Mit dem Ansatz aus a) ergibt sich:
r = $\sqrt{\frac{\mathrm{GM}}{g}}$
=> r = 1.740.038,4 m

Aufgabe 4) Wasserstoff-Atome
a) Die Masse des Wasserstoffatoms setzt sich aus einer Protonenmasse und einer Elektronenmasse zusammen.
m_H= 1,67E-26kg + 9,1E-31kg=1,67E-26kg
Die Elektronenmasse spielt also kaum eine Rolle.
Die Gravitationskraft berechnet sich aus dem Newtonschen Gravitationsgesetz:
F_G=G $\frac{\mathrm{m_H²}}{\mathrm{r²}}$ = 1,84E-60N

b) Für die Beschleunigung gilt:
a = F/m = 1,1E-34N
Gehen wir von einer gleichförmig beschleunigten Bewegung aus, so können wir ansetzen:
s = 1/2 a t², also
t = $\sqrt{\frac{\mathrm{2s}}{a}}$ = 4,26 s
Dies entsprichet einer Zeit von 1,35 Mrd Jahren.

c) Da der Radius mit der Zeit abnimmt steigt mit der Zeit auch die Gravitationskraft und damit die Beschleunigung. Die Atome bewegen sich also schneller aufeinander zu als in unserer Abschätzung.
Damit nimmt die Zeit bis zum Zusammenprall ab.
Anmerkung:
Um unser Problem exakt zu lösen müsste man eine Differentialgleichung der Form y'' ~ 1/y^2 lösen.
So einfach diese Gleichung aussehen mag, die Lösung ist es keineswegs!!!

zurück home inhalt