Lösung: A-0017

Bohrsches Wasserstoffatom

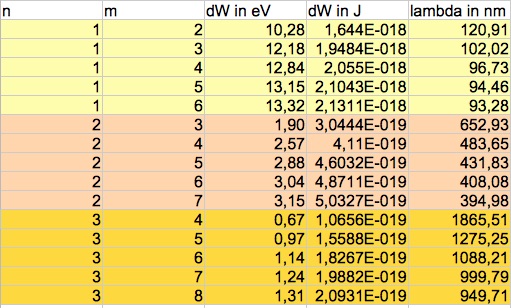
Aufgabe 1: Energiedifferenz aus: ΔW = W0 $(\frac{1}{n^2}-\frac{1}{m^2})$mit m,n∈ℕ, m>n Wellenlänge aus: λ = hc/ΔW

Aufgabe 2:
a) λ = hc/ΔW = 91,35 nm
b) W_kin = 16eV - 13,6 eV = 2,4 eV = 3,84E-19 J
v = 9,2E5 m/s
c) Das Elektron wird zunächst auf das 2. Niveau angehoben und verbleibt dort kurz. Wird es während dieses Aufenthaltes wieder von einem Photon getroffen, so findet Ionisierung statt.
d) Die kinetische Energie des Elektrons beträgt:
W_kin= 1/2 m v² = 4,095 E-16 J = 2559,375 eV
Die Ionisierungsenergie beträgt 13,6 eV.
Damit sind 188 Ionisierungen möglich. Befinden sich nicht alle Elektronen im Grundzustand, sind auch mehr Ioniserungen möglich.

zurück home inhalt