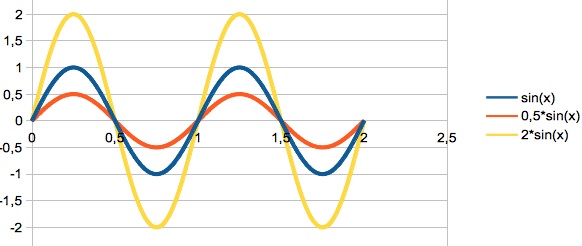
Die Amplitude steht als Zahlenfaktor vor der Sinusfunktion und gibt ihre Höhe an.
Es gilt f(x) = A*sin(x)
Physikalisch stellt diese Höhe die Intensität einer Schwingung, z.B. ihre Lautstärke dar.
Grundlagen: Sinusfunktion
Üblicherweise wird eine Schwingung über eine Sinusfunktion beschrieben. Eine
Cosinusfunktion ist ebenfalls möglich aber unüblicher.
| Amplitude Höhe der Schwingung Die Amplitude steht als Zahlenfaktor vor der Sinusfunktion und gibt ihre Höhe an. Es gilt f(x) = A*sin(x) Physikalisch stellt diese Höhe die Intensität einer Schwingung, z.B. ihre Lautstärke dar. |
|
| Frequenz Schnelligkeit der Schwingung Die Frequenz steht als Zahlenfaktor im Argument der Sinusfunktion. Dabei wird noch der Faktor 2π ergänzt. Es gilt f(x) = sin(2π*f*x) Physikalisch stellt die Frequenz die Häufigkeit einer Schwingungsbewegung dar, z.B. in Form der Tonhöhe. |
 |
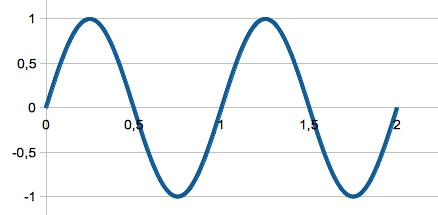
| Einheitsschwingung Amplitude und Frequenz gleich
eins Es gilt f(x) = 1*sin(1*2π*x) |
 |