Heisenbergsche Unschärferelation 2

Energie-Zeit-Relation

Grundlagen: Energie-Zeit-Realtion
Eine weitere Schreibweise der Heisenbergschen Unschärferelation lautet:
ΔW Δt > h/4π
D.h. das Produkt aus der Unschärfe einer Energiemessung und einer Zeitmessung kann einen (sehr kleinen) Wert nicht unterschreiten.

Herleitung: Wir wissen bereits:
Δx Δp > h/4π
Erweitern mit $\frac{\Delta t}{\Delta t}: \Delta p·\frac{\Delta t}{\Delta t}·\Delta x \ge \frac{\sout{h}}{2}$
Umsortieren: $\Delta t·\frac{\Delta p}{\Delta t}·\Delta x \ge \frac{\sout{h}}{2}$
$\frac{\Delta p}{\Delta t}$ ist aber gerade eine Definition der Kraft F.
F Δx ist aber gerade ΔW. Also:
ΔW Δt $\ge \frac{\sout{h}}{2}$

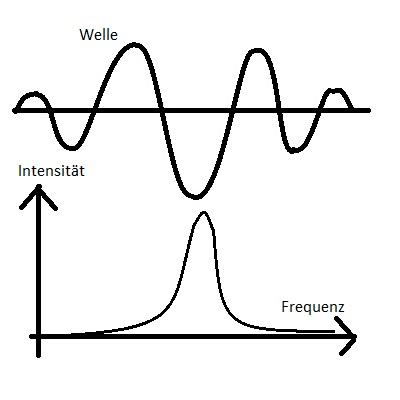
Folgerung 1: Unschärfe der Photonenfrequenz Wird ein Photon ausgesandt, so ist dieser Vorgang zeitlich begrenzt. Daher kann man ein Photon nicht als unendlich ausgedehnte Welle sondern als begrenzten Wellenzug verstehen. Durch mathematische Methoden (Fourier-Analyse) lässt sich zeigen, dass dies nur möglich ist, wenn die Welle aus einer Vielzahl sich überlagernder Wellenzüge unterschiedlicher Frequenz besteht. Genauer handelt es sich um die Überlagerung unendlich vieler Wellen in einem bestimmten Frequenzbereich. a) Der Aussendungsprozess eines Photons der Energie 2eV dauere 1ps. Wie groß ist dann seine Energieunscharfe? b) In welchem Bereich liegt der Hauptteil seiner Frequenzen? c)Wie kurz hätte der Prozess sein dürfen, damit die Energieunschärfe 10% nicht übersteigt? d) Vergleichen Sie für diesen Fall die Unschärfe der Schwingungsdauer mit der mittleren Schwingungsdauer der Welle. Was bedeutet dies für die Wellenform?

Folgerung 2: Unschärfe der Zeitmessung
Atomuhren sind in der Lage, extrem kurze Zeitabschnitte sehr genau zu messen. Dazu werden Photonen verwendet, die bei einem Elektronenübergang in einem Cäsiumgas (ΔW = 3,79 E-5 eV) entstehen.
a) Welche Energie müssen die Photonen mindestens haben, wenn eine Genauigkeit der Zeitmessung von Δt = 2,0 E-15 sec (1fs) erreicht werden soll?
b) Welche Frequenz und Schwingungsdauer haben diese Photonen? Vergleichen Sie mit der geforderten Genauigkeit.

Folgerung 3: Der Energieerhaltungssatz gilt nicht streng!
Durch die Unschärferelation können minimale Verstöße im Energieerhaltungssatz erlaubt sein.
a) Ein physikalisches System wird über 3 Stunden beobachtet. Es soll herausgefunden werden, ob der Energieerhaltungssatz wirklich gilt. Wie genau kann die Messung bestenfalls sein?
b) Wie lang könnte ein Physikalisches System um 1pJ vom Energieerhaltungssatz abweichen, ohne dass man es bemerken könnte?

zurück home inhalt pdf Lösungen