Interferenz

Nachweis von Welleneigenschaften

Grundlagen: Eigenschaften von Wellen

Wellen werden durch folgende Eigenschaften gekennzeichnet:
- die Wellenlänge λ: räumlicher Abstand zwischen zwei Punkten gleicher Intensität und gleicher Intensitätsänderung
- die Frequenz f: zeitlicher Abstand zwischen zwei Punkten gleicher Intensität und gleicher Intensitätsänderung
- die Ausbreitungsgeschwindigkeit c: Bewegungsgeschwindigkeit eines beliebigen Punktes in Ausbreitungsrichtung

Die drei Größen hängen voneinander ab. Es gilt c = λ f

Außerdem wird die Strärke einer Welle als Intensität I angegeben.

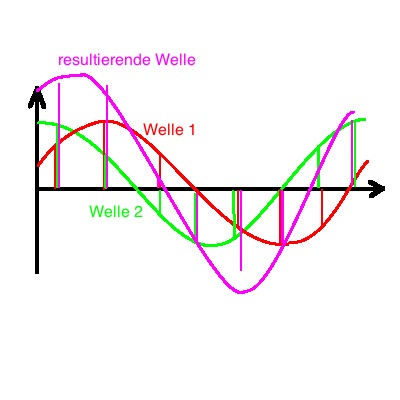
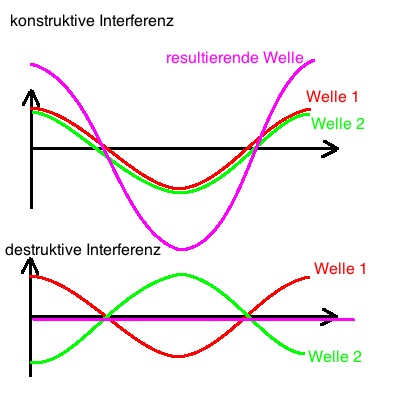
Interferenz 1: Überlagerung, Verstärkung und Auslöschung Das Phänomen der Interferenz im engeren Sinne tritt nur bei Wellen auf, die gleiche Wellenlänge, Ausbreitungsgeschwindigkeit und Frequenz haben und deren Intensitäten gleich sind. Treffen zwei solche Wellen aufeinander, so überlagern sie sich, d.h. ihre Intensitäten addieren sich. (Bild 1) Treffen dabei zwei Wellenberge oder zwei Wellentäler aufeinander, so verstärken sich die Intensitäten. (konstruktive Interferenz) Treffen Wellental und Wellenberg aufeinander, so löschen sich die Intensitäten aus. (destruktive Interferenz) (Bild 2)

Interferenz 2: Verschiebung Sind sich zwei Wellen in der oben beschriebenen Weise ähnlich, d.h. sind λ, f und c gleich, so können sie sich dennoch dadurch unterscheiden, dass sie gegeneinander Verschoben sind. Diese Verschiebung φ kann entweder in Grad bzw. Bogenmaß angegeben werden, wobei eine Wellenlänge 360° bzw. 2π entspricht, oder man bezieht sich auf einen Bruchteil oder ein Vielfaches der Wellenlänge. Beispiele für Verschiebungen: φ in ° φ in rad φ bezügl. λ 0 0 0 10 0,31415 1/36 λ 90 π/2 1/4 λ 180 π 1/2 λ 360 2π λ Konstruktive Interferenz liegt genau dann vor, wenn φ ein ganzzahliges Vielfaches von 360°, 2π bzw. der Wellenlänge ist, also 0, 1, 2, 3, ... Destruktive Interferenz liegt genau dann vor, wenn das Vielfache halbzahlig ist, also 0.5, 1.5, 2.5, ...

Interferenz 3: Verschiebung bei Beugung Zwei Wellen laufen zunächst mit φ=0 absolut parallel nebeneinander her. Ändern sie nun z.B. durch Beugung die Richtung, so erhalten sie nun eine Phasenverschiebung φ≠0. Ist der Abstand der beiden Wellen a und der Beugungswinkel α, so gilt für die Phasenverschiebung: Δλ = a sin(α) Konstruktive Interferenz tritt auf, wenn n λ = a sin(α) mit n∈ℕ0 Destruktive Interferenz tritt auf, wenn (n+1/2) λ = a sin(α) mit n∈ℕ0

zurück home inhalt