Der ohmsche Widerstand ist ein konstanter Wert, der das Verhältnis von Strom und Spannung angibt.
Strom und Spannung sind in Phase, d.h. nicht gegeneinander verschoben.
Kombination von Ohmschen, induktiven und kapazitativen Widerständen
Grundlagen: Widerstandsgleichungen
Der Widerstand ist definiert als der Quotient aus Spannung und Strom: R = U/I,
d.h. er sagt aus, wie viel Spannung U nötig ist, damit ein Strom der Stärke I
durch ein bestimmtes Bauteil fließen kann.
Für den Wechselstromkreis bezieht sich der Widerstand auf die Aplituden von
Strom und Spannung. R = U0/I0
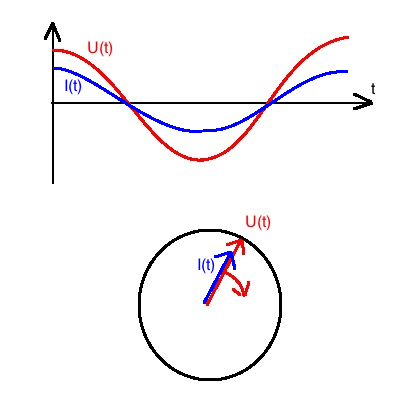
| Ohmscher Widerstand RΏ: Der ohmsche Widerstand ist ein konstanter Wert, der das Verhältnis von Strom und Spannung angibt. Strom und Spannung sind in Phase, d.h. nicht gegeneinander verschoben. |
|
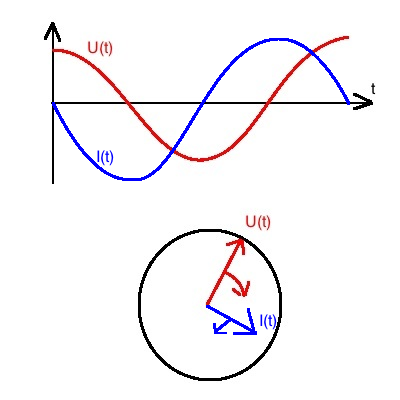
| Kapazitativer Widerstand RC: Der kapazitative Widerstand ist frequenzabhängig. Es gilt: RC=1 / ωC, d.h. je größer die Frequenz, desto geringer ist der Widerstand. Dies ist insofern logisch, da sich der Kondensator bei hohen Frequenzen kaum aufladen wird und daher auch keinen Widerstand entgegensetzen kann. Strom und Spannung sind um T/4 gegeneinander verschoben, so dass der Strom der Spannung vorauseilt. Dies ist insofern logisch, da sich der Kondensator zunächst durch einen Strom aufladen muss, damit er eine Spannung hat. |
|
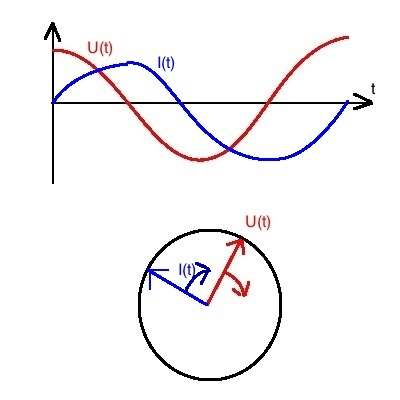
| Induktiver Widerstand RL: Der induktive Widerstand ist frequenzabhängig. Es gilt: RC=ωL, d.h. je größer die Frequenz, desto größer ist der Widerstand. Dies ist insofern logisch, da die Spule bei hohen Frequenzen hohe Spannungen induziert und somit einen hohen Widerstand entgegensetzen kann. Strom und Spannung sind um T/4 gegeneinander verschoben, so dass der Strom der Spannung hinterhereilt. Dies ist insofern logisch, da ein Anwachsen des Stromes sofort eine Induktionsspannung erzeugt. |
|