Lorentzkraft bei Strömen und Teilchen

Reduzierung des Stromes auf die Bewegung eines Teilchens

Grundlagen Definition der magnetischen Flussdichte und des Stromes
Die Magnetische Flussdichte B ist definiert durch die Lorentzkraft F_L auf einen Strom I entlang eines Leiterstückes der Länge s:
F = B I s <=> B = $\frac{F}{Is}$
Der Strom ist definiert als die Änderung der vorhandenen Ladung, also als eine Bewegung von Ladungen:
I = $\frac{\mathrm{\Delta Q}}{\mathrm{\Delta t}}$

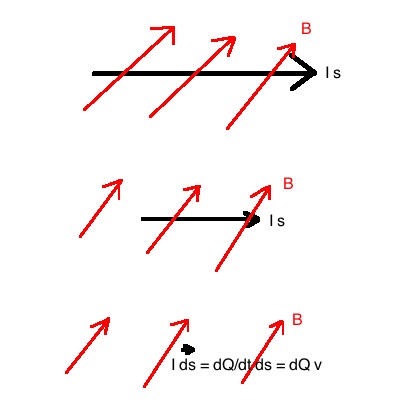
Lorentzkraft auf eine bewegte Punktladung: Grenzwertbildung Wie groß ist die Lorentzkraft auf ein einzelnes (punktförmiges) geladenes und bewegtes Teilchen? Das Problem wird durch einen Grenzwert gelöst: Viele Teilchen entlang eines Leiters bilden eines Strom I der Länge s. Für sie gilt: F = B I s. Lässt man nun die Länge des Leiters gegen Null gehen, d.h. s→Δs gilt: F = B I Δs Ersetzt man nun den Strom I durch den Quotienten I = $\frac{\mathrm{\Delta Q}}{\mathrm{\Delta t}}$, so erhält man: F = B $\frac{\mathrm{\Delta Q}}{\mathrm{\Delta t}}$Δs oder durch Umsortierung: F = B ΔQ $\frac{\mathrm{\Delta s}}{\mathrm{\Delta t}}$= B ΔQ v

zurück home inhalt