Die Kepplerschen Gesetze

Expertenlenrnen

Vorgehensweise: Wählen Sie eine der folgenden Stationen aus und erarbeiten Sie diese. Stellen Sie anschließend Ihren Mitschülern die Ergebnisse vor.

Grundlagen: Drei Gesetze beschreiben die Planetenbewegung
Die drei Kepplerschen Gesetze lauten:

1) Alle Planeten bewegen sich auf Ellipsenbahnen, in deren einen Brennpunkt die Sonne steht.
2)Der Fahrstrahl zwischen Sonne und Planet überstreicht in gleichen Zeiten gleiche Flächen.
3)Die Quadrate der Umlaufzeiten zweier Planeten verhalten sich zueinander wie die dritten Potenzen (Kuben) der mittleren Abstände.

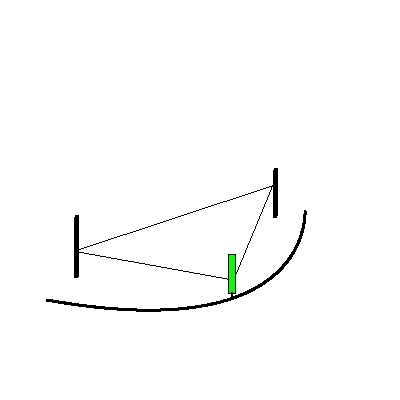
1. Gesetz Ellipsenbahnen Ellipsenbahnen entstehen z.B. durch folgende Konstruktion: - Fixieren Sie zwei Nägel auf einem Brett. - Legen Sie eine Schlaufe aus Bindfaden um diese zwei Nägel. - Bilden Sie nun mit einem Stift aus der Schlaufe ein Dreieck und zeichnen Sie die entstehende Bahn nach. 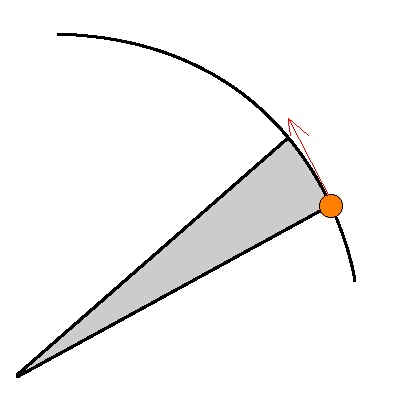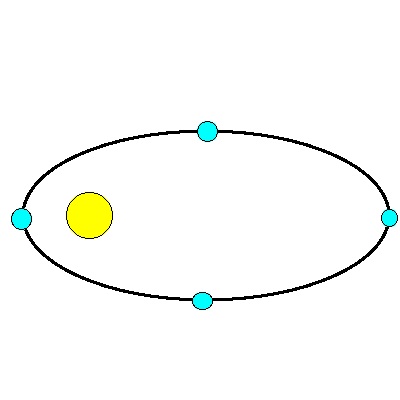Aufgabe: Zeichnen Sie mehrere solcher Ellipsen für verschiedene - Fadenlängen (Veränderung der Achsenlänge) - Nagelabstände (Veränderung der Exzentrität) Diskutieren Sie: Ein Nagel entspricht der Sonnenposition. Er ist für alle Bahnen also gleich. Können sich dann Planetenbahnen kreuzen? Versuchen Sie eine entsprechende Konstruktion.

2. Gesetz Fahrstrahl Das Gesetz hängt eng mit der Drehimpulserhaltung zusammen. Aufgabe: Ein Planet mit der Geschwindigkeit v, der Masse M und der Entfernung zur Sonne R überstreicht in der Zeit Δt eine Fläche. Zeigen Sie, dass diese Fläche gerade dem Drehimpuls entspricht. Diskutieren Sie: Die Jahreszeiten werden in der Astronomie durch die Tag- und Nacht-Gleichen bzw. durch den längsten und kürzesten Tag des Jahres begrenzt. Zur Zeit liegen diese Termine am 20.3.2013, 21.6.2013, 22.9.2013 und am 21.3.2014. Sie entsprechen der Position der Erde auf dem nebenstehenden Bild. Was sagt Ihnen die Länge der einzelnen Jahreszeiten (in Tagen) über die Position der Erde?

3. Gesetz Verhältnis von Radien und Umlaufzeiten Das Kepplersche Gesetz lässt sich auf zwei Arten schreiben: $\frac{{T_1}^2}{{T_2}^2}=\frac{{R_1}^3}{{R_2}^3}$ oder als T2∼R3 Tatsächlich kann man diese zweite Formulierung des 3. Kepplerschen Gesetzes direkt aus dem Newtonschen Gravitationsgesetz zusammen mit der Zentralkraft herleiten. Aufgabe 1) Zeigen Sie dies. Welche Größen stecken in der Proportionalitätskonstante? Berechnen Sie sie. Aufgabe 2) Zeigen Sie anhand einiger Planeten die Gültigkeit dieses Gesetzes. Die Daten finden Sie in der nebenstehenden Tabelle.

Planet Umlaufzeit Große Halbachse Erde 365,256d 1AE Merkur 87,969d 0,387099AE Jupiter 4332,588d 5,202803AE Mars 686,9798d 1,523691AE Neptun 60187,64d 30,05708AE

1AE = 149,6 E6 km
Überprüfen Sie auch die oben theoretisch berechnete Konstante.

zurück home inhalt Lösungen