massendefekt

Grundlagen: Energie-Massen-Equivalent

Albert Einstein fand in seiner speziellen Relativitätstheorie 1905 nicht nur heraus, dass Raum und Zeit einander beeinflussen (relativ zueinander sind), er fand auch seine berühmte Gleichung E = m c², nach der Energie und Masse über eine Konstante miteinander verbunden sind, d.h. proportional zueinander sind.
Eine wichtige Folgerung war, dass sich Masse in Energie umwandeln lassen müsste. Diese Erkenntnis führte schnell zu Überlegungen, dass sich aus Prozessen der Kernspaltung und -fusion große Mengen an Energie gewinnen lassen müssen.

Das Prinzip des Massen-Energie-Equivalentes findet man auch in anderen Prozessen, aber nur in Kernumwandlungsprozessen wird genügend Energie umgewandelt, so dass der Effekt messbar wird.

Kernumwandlungen als exotherme Prozesse

Wenn sich zwei Nukleonen (Neutronen oder Protonen) einander annähern, setzt ab einem sehr geringen Abstand die Starke Wechselwirkung ein. Sie erzeugt eine starke bindende Kraft zwischen den Nukleonen, die dafür sorgt, dass der entstandene Atomkern zusammenhält, auch wenn er mehrere positiv geladene Protonen enthält.

Dieser Prozess der Bindung ist exotherm, d.h. er geht einher mit der Abgabe von Energie.

Verschmelzung von zwei Nukleonen unter Energieabgabe

Potentialtopfmodell

Dieser Prozess lässt sich auch im Potentialtopfmodell darstellen. Die Nukleonen nähern sich einander an, bilden einen gemeinsamen Potentialtopf und "fallen" in diesen hinein. Dabei wird Energie frei.

Das Modell funktioniert auch bei der Annäherung von zwei Protonen. Dabei muss aber die gegenseitige Abstpoßung berücksichtigt werden, d.h. die Nukleonen müssen zunächst einen Potentialberg "hinaufklettern".
Dabei kommt es zu einer typisch quantenmechanischen Besonderheit: Statt den gesamten Berg überwinden zu müssen ist es den Protonen aufgrund ihrer Welleneigenschaften möglich, ihn mit einer gewissen Wahrscheinlichkeit zu durchdringen. Man spricht von einer Durchtunnelung.

Nukeonen fallen in Potentialtopf und geben Energie ab

Protonen klettern den Potentialberg hoch, durchtunneln ihn, fallen in einen Potentialtopf und geben Energie ab

Massendefekt

Diese Vorgänge gehen einher mit einem zusätzlichen Effekt. Die Energieabgabe erfolgt gleichzeitig mit einer Massenabnahme. D.h. nach der Abgabe der Energie ist die Masse der Nukleonen geringer als vorher. Masse ist in Energie umgewandelt worden.

Die frei gewordene Energie bei der Zusammenstellung des Atomkerns aus den einzelnen Nukleonen lässt sich wie folgt berechnen:
Zunächst ermittelt man aus der Ordnungs- und Massenzahl die Anzahl der Protonen und Neutronen in einem Atomkern. Diese multipliziert man mit der Masse eines freien Neutrons bzw. Protons und addiert die beiden Werte.
m_{einzelne Nukeonen} = m_p*p + m_n*n
Durch Untersuchungen mit einem Massenspektrometer kann man die tatsächliche Masse des Atomkerns bestimmen. Subtrahiert man die Masse der einzelnen Nukeonen mit dieser tatsächlichen Masse, so erhält man den sogenannten Massendefekt.
Δm = m_{einzelne Nukleonen} - m_tatsächlich
Über Einsteins berühmte Gleichung E = mc² erhält man nun die freigewordene Energie. ΔW = Δm c²

Waage mit Nukleonen, rechts nähern sie sich an und werden leichter, Waagschale geht nach oben.

Bindungsenergie pro Nukleon Wie viel ENergie wurde bei der Bildung eines Kerns frei?

Für jedes Isotop jedes Elementes lässt sich so die frei gewordene Energie bei der Zusammenstellung aus den einzelnen Nukleonen berechnen.

Teilt man diese frei gewordene Energie durch die Anzahl der Nukeonen, so erhält man die Bindungsenergie pro Nukleon. Diese ist ein interessanter Wert für die Stärke der Bindung der Nukleonen im Kern.

Im nebenstehenden Diagramm erkennt man, dass die Bindungsenergie für das Wasserstoffisotop Deuterium (je ein Proton und Neutron) besonders niedrig ist. Zur Massenzahl 56 (Eisen) hin steigt der Wert an, danach fällt er wieder ab.

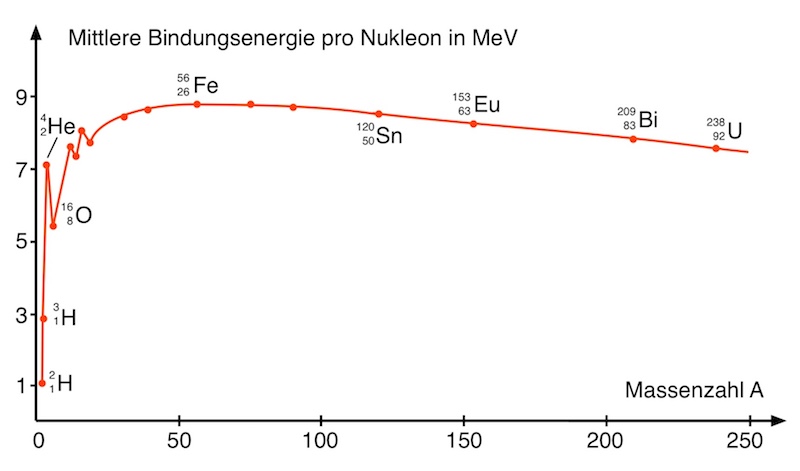
Exotherme Kernumwandlungen Welche Fusions- bzw. Spaltungsprozesse laufen exotherm, d.h. unter Energiefreigabe, ab?

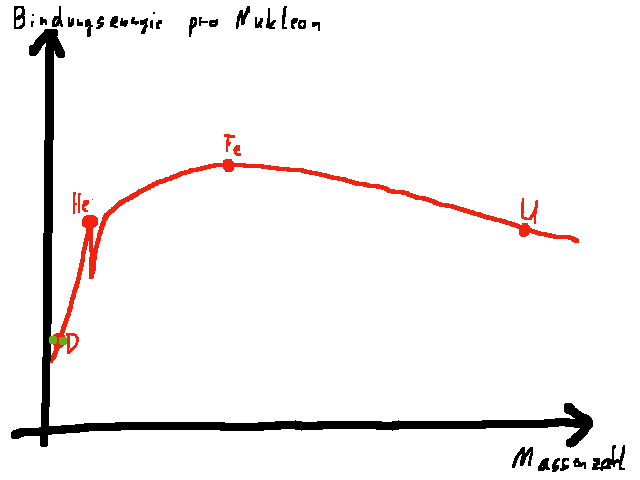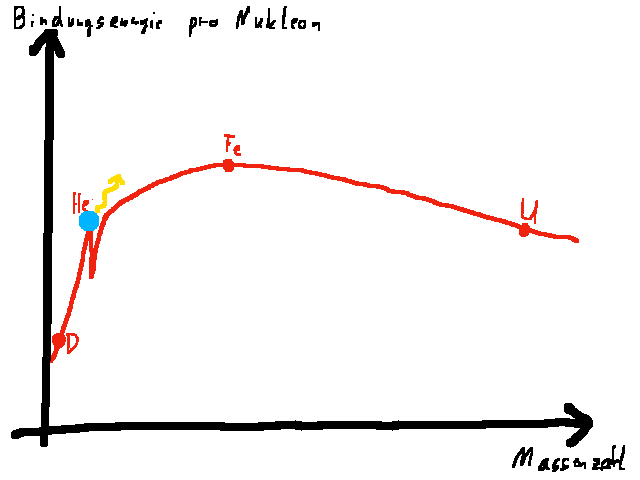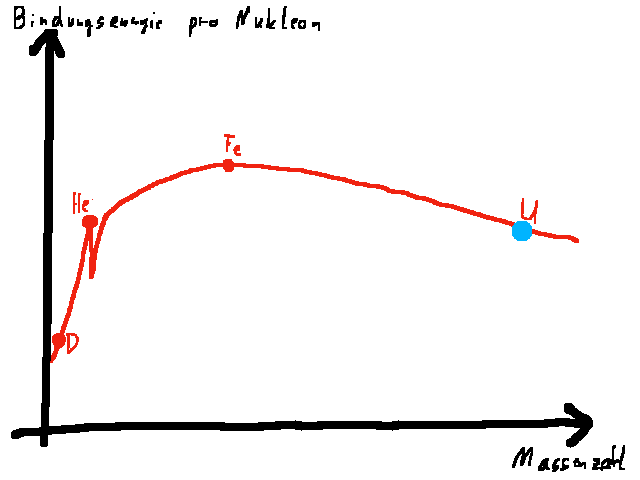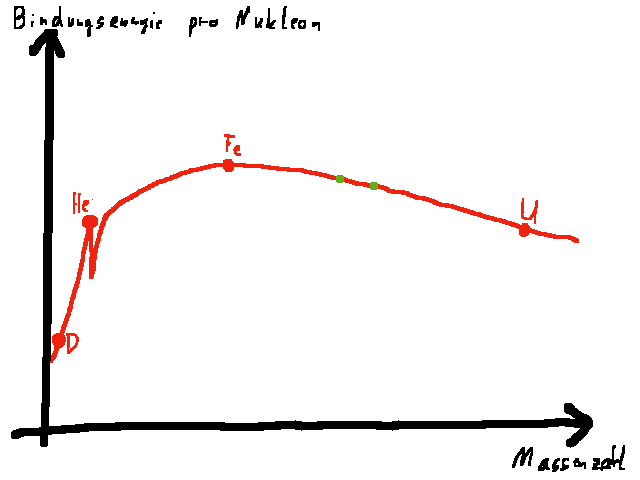
Die Bindungsenergie pro Nukleon zeigt uns, welche Kernumwandlungsprozesse exotherm, d.h. unter Abgabe von Energie ablaufen. Dies ist immer dann der Fall, wenn die mittlere Bindungsenergie pro Nukleon steigt. Wir unterscheiden zwei Fälle:

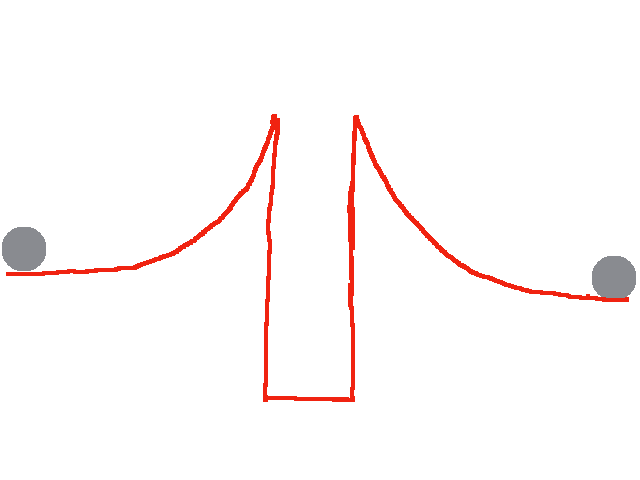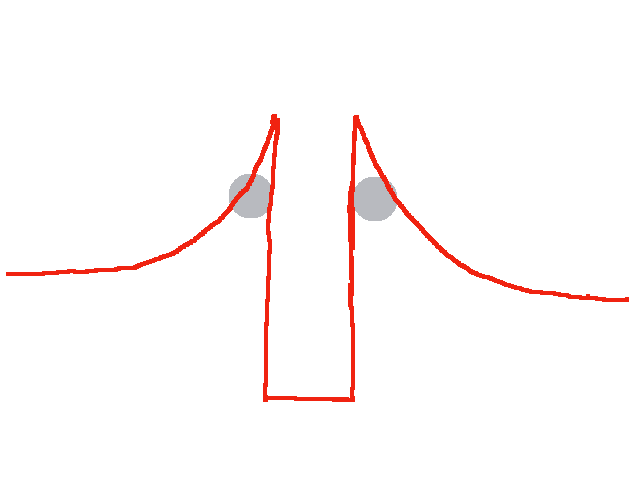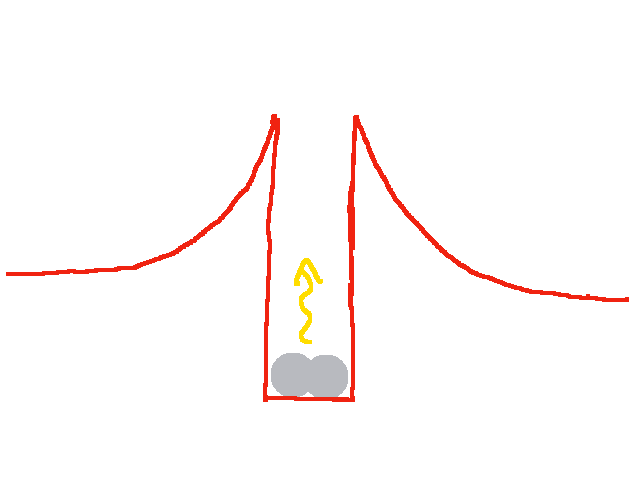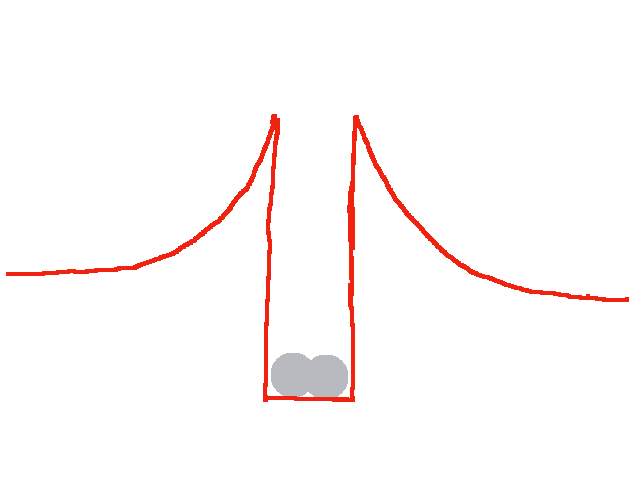
Verschmelzung von Kernen (Kernfusion): Diese verläuft nur für Kerne, die kleiner als Eisen sind, exotherm.
Besonders effektiv, d.h. mit besonders großer Freisetzung von Energie, ist dabei die Verschmelzung von zwei Deuteriumkernen zu Helium. Aber auch die Verschmelzung von zwei Heliumkernen zu einem Berilliumkern oder von zwei Lithiumkernen zu einem Kohlenstoffkern verläuft exotherm.
Kernspaltung: Diese verläuft nur für Kerne, die größer als Eisen sind, exotherm.
Insbesondere gilt dies für besonders große Kerne wie Uran, die sich in zwei deutlich kleinere Kerne umwandeln. Dieser Prozess wird in Kernreaktoren (Atomkraftwerken) ausgenutzt.

Wir müssen noch einige Besonderheiten beachten:

Die oben gemachten Aussagen gelten u.U. nicht mehr, wenn die Eisengrenze beim Umwandlungsprozess überschritten wird, z.B. wenn zwei Kerne knapp unter der Massenzahl von Eisen zu einem Kern mit höherer Massenzahl als Eisen verschmelzen, oder wenn ein Kern mit nur wenig höherer Massenzahl als Eisen gespalten wird.
Offenbar ist ein Heliumkern unter den kleinen Atomkernen besonders stabil. Dies erklärt, warum es bei großen Atomkernen besonders häufig zu einem Alphazerfall kommt um sich zu verkleinern. Eine Abspaltung eines Lithiumkernes o.ä. wäre zwar auch denkbar aber aufgrund der weniger großen Stabilität wesentlich unwahrscheinlicher.