Zerfalls- und Schwächungsgesetz

Herleitung aus einer Differentialgleichung

Zerfallsgesetz:
Zur Herleitung müssen wir lediglich zwei einfache Annahmen machen:

Die Anzahl der Zerfälle ist proportional zur Anzahl der vorhandenen Atome und zur verstrichenen Zeit. Die Änderung ist wegen der Abnahme der Atomzahl negativ.
Es gilt: dN~N · dt
Innerhalb der Halbwertzeit T_1/2 halbiert sich die Anzahl der noch vorhandenen Kerne durch Zerfall.
Es gilt: N(T_1/2) = 1/2 N₀.

Die Annahme 1 kann man auch folgendermaßen lesen:

\frac{dN}{dt} =

- c · N
d.h. gesucht ist eine Funktion N(t), deren Ableitung die Funktion selber multipliziert mit einem negativen Vorfaktor ergibt.
Dies gilt für alle Exponentialfunktionen mit negativem Exponenten, insbesondere für die e-Funktion. D.h. es muss gelten:

{N (t) = N_{0} \cdot e}^{- c t}

Der Faktor c ergibt sich aus der Überlegung 2.
Es soll gelten:
N(T_1/2) =

N_{0} e^{- c T_{1 / 2}}

= 1/2 N₀ ⇔

e^{- c T_{1 / 2}} = \frac{1}{2}

⇔
-cT_1/2 = ln(1/2)
Umstellen ergibt:
c =

- \frac{\ln (1/2)}{T_{1 / 2}}

\frac{\ln (2)}{T_{1 / 2}}

Damit folgt als endgültige Form des Zerfallsgesetzes:
N(t) = N₀

e^{\frac{- t \cdot \ln (2)}{T_{1 / 2}}}

Schwächungsgesetz 1: Absorbtionsgesetz
Zur Herleitung müssen wir lediglich zwei einfache Annahmen machen:

Die Anzahl der abgefangenen Strahlungsteilchen ist proportional zur Ursprünglichen Anzahl und zur zurückgelegten Strecke. Die Änderung ist wegen der Abnahme der Strahlungsteilchen negativ.
Es gilt: dA~A · dx
Innerhalb der Halbwertdicke d_1/2 halbiert sich die Anzahl der noch vorhandenen Kerne durch Zerfall.
Es gilt: A(d_1/2) = 1/2 A₀.

Die Annahme 1 kann man auch folgendermaßen lesen:

\frac{dA}{dt} =

- c · A
d.h. gesucht ist eine Funktion A(x), deren Ableitung die Funktion selber multipliziert mit einem negativen Vorfaktor ergibt.
Dies gilt für alle Exponentialfunktionen mit negativem Exponenten, insbesondere für die e-Funktion. D.h. es muss gelten:

{A (x) = A_{0} \cdot e}^{- cx}

Der Faktor c ergibt sich aus der Überlegung 2.
Es soll gelten:
A(d_1/2) =

A_{0} e^{- c d_{1 / 2}}

= 1/2 A₀ ⇔

e^{- c d_{1 / 2}} = \frac{1}{2}

⇔
-cd_1/2 = ln(1/2)
Umstellen ergibt:
c =

\frac{\ln (2)}{d_{1 / 2}}

Damit folgt als endgültige Form des Schwächungsgesetzes:
A(t) = A₀

e^{\frac{- x \cdot \ln (2)}{d_{1 / 2}}}

Schwächungsgesetz 2: Abstandsgesetz

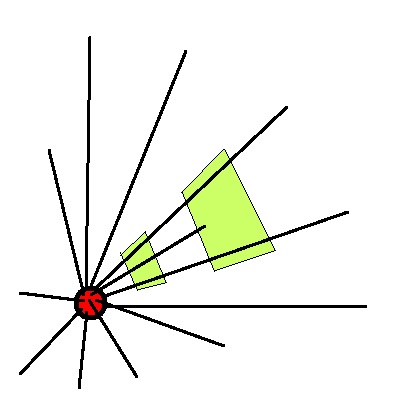
Betrachtet man die Strahlung als ein divergierendes Bündel aus Lichtstrahlen oder Teilchen, so ergibt sich folgende Überlegung:
Vergrößert man den Abstand von der Quelle, so verteilen sich die Strahlungsteilchen auf eine immer größere Fläche. Damit nimmt die Aktivität pro Flächeneinheit ab.
Da die Fläche mit dem Abstand quadratisch wächst gilt insbesondere:
A(r)~1/r² oder A(r) = A₀ 1/r² mit A₀: gemessene Aktivität pro Flächeneinheit im Abstand 1(m).

zurück home inhalt