Verteilung der Elektronen auf die einzelnen Schalen eines Atoms
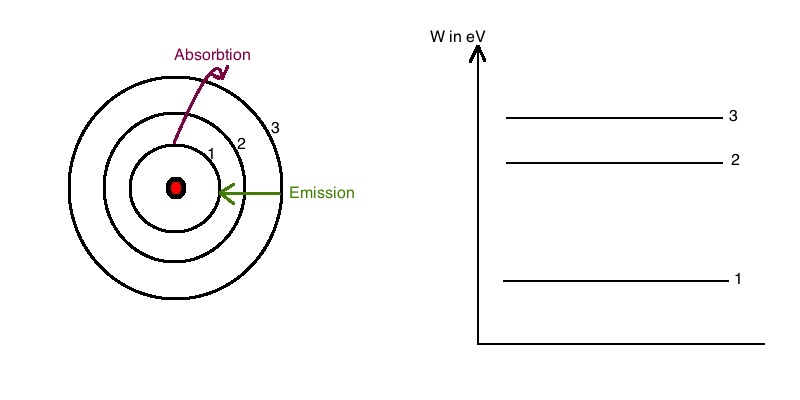
| Schalenstruktur: diskrete Energiezustände Innerhalb eines Atoms können die Elektronen nur bestimmte Energiezustände einnehmen. Sie können zwischen diesen Energiezuständen wechseln, wenn sie Energie aufnehmen (Absorbtion) oder abgeben (Emission). Dem Energieniveau wird eine natürliche Zahl n zugeordnet, die Hauptquantenzahl genannt wird. Die Schalen werden mit den Buchstaben k, l, m, ... bezeichnet.
|
|
| Orbitale: Form der Schalen Genauere quantenmechanische Betrachtungen zeigen, dass sich die Elektronen nicht auf kreisförmigen Bahnen sondern auf wolkenförmigen Orbitalen befinden, d.h. man kann Raumbereiche bestimmen, in denen sich die Elektronen mit hoher Wahrscheinlichkeit aufhalten, ohne genaue Angaben über Ort und Bewegungsrichtung (Impuls) machen zu können. Diese Raumbereiche sind kugelförmig (s) oder haben die Form von Hanteln (p), gekreuzten Hanteln (d) oder noch komplexeren Gebilden (f,g, ...) Der Form des Orbitals wird eine natürliche Zahl l zugeordnet, die Nebenquantenzahl genannt wird. Es gilt:
|
gif
gif
gif
|
| Orbitalrichtung: Orientierung der Orbitale Bei den verschiedenen Orbitalen sind außerdem verschiedene Ausrichtungen möglich. Diese Ausrichtung ist insofern wichtig, als dass die sich im Orbital befindlichen Elektronen einen magnetischen Dipol erzeugen. Diese Quantenzahl wird daher als magnetische Quantenzahl m bezeichnet. s: Das s-Orbital ist als Kugel vollkommen symmetrisch. Daher gibt es keine bevorzugte Ausrichtung. Das s-Orbital hat die Orientierung m=0. p: Die p-Orbitale können in x-, y- und z-Richtung orientiert sein. Blickt man aus der y-Richtung auf die Orbitale, so ist das in y-Richtung orientierte wieder symmetrisch (Orientierung m=0), den beiden anderen Richtungen werden die Orientierungen m=1 und m=-1 zugeordnet. d: Es sind 5 Orientierungen m möglich, die von -2 bis 2 gezählt werden. |
|
| Spin: Drehimpuls der Elektronen Schließlich können die Elektronen selber noch genau zwei Zustände innerhalb eines Orbitals einnehmen. Diese beiden Zustände verhalten sich so, als würden sich die Elektronen wie kleine Kugeln um ihre eigene Achse drehen. Daher wird diese Quantenzahl s (spin) genannt. Sie kann die Werte s=1/2 und s=-1/2 einnehmen. |
|
Pauli-Prinzip: Einzigartigkeit der
Elektronenzustände
Das Pauli-Prinzip lautet:
In einem Atom kann jedes Elektron nur einen einzigartigen Zustand
einnehmen, d.h. es muss sich in mindestens einer Quantenzahl von den anderen
Elektronen unterscheiden.
Genauer gesagt gilt dieses Prinzip nicht nur innerhalb eines Atoms, sondern
lässt sich auf einfache und komplexe Moleküle bis hin zu Festkörpern mit
unzählig vielen Elektronen erweitern.
Weiterhin gilt: